题目内容
3.已知2α2+2α=1,2β2+2β=1,求|α-β|的值.分析 由于2α2+2α-1=0,2β2+2β-1=0,于是可把α、β看作方程2x2+2x-1=0的两根,然后利用根与系数的关系得到α+β=-1,αβ=-1,然后利用整体代入的方法计算.
解答 解:∵2α2+2α-1=0,2β2+2β-1=0,
∴α、β可看作方程2x2+2x-1=0的两根,
∴α+β=-1,αβ=-1,
∴|α-β|=$\sqrt{(α+β)^{2}-4αβ}$=$\sqrt{5}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两个根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知弧AB和弧CD的度数分别为90°和50°,则∠P=20°.
如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知弧AB和弧CD的度数分别为90°和50°,则∠P=20°.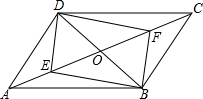 如图,?ABCD中,对角线AC、BD相交于点O,若BD=12cm,AC=20cm
如图,?ABCD中,对角线AC、BD相交于点O,若BD=12cm,AC=20cm