题目内容
8.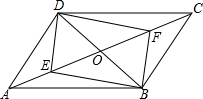 如图,?ABCD中,对角线AC、BD相交于点O,若BD=12cm,AC=20cm
如图,?ABCD中,对角线AC、BD相交于点O,若BD=12cm,AC=20cm(1)现E从A出发以1cm/s的速度向C运动,同时F从C出发以2cm/s的速度向A运动.当E与F相遇前,四边形DEBF是平行四边形吗?会的话,求出运动的时间t,不会的话说明理由;
(2)现E从A出发以1cm/s的速度向C运动,F从C出发以acm/s的速度向A运动,且F比E晚2秒钟,当E与F相遇前,以D、E、B、F为顶点的四边形是否是矩形?是的话,请求时间t和a的值.
分析 (1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由E从A出发以1cm/s的速度向C运动,同时F从C出发以2cm/s的速度向A运动,易得2AE=CF,即可得OE≠OF,则可判定四边形DEBF不是平行四边形;
(2)若以D、E、B、F为顶点的四边形是矩形,则需要满足两个人条件一是EF=BD,OE=0F,由此建立关于a和t的方程组,解方程组即可求出a和t的值.
解答 解:(1)四边形DEBF不是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E从A出发以1cm/s的速度向C运动,同时F从C出发以2cm/s的速度向A运动.
∴2AE=CF,
∴OE≠OF,
∴四边形DEBF不是平行四边形;
(2)当E与F相遇前,以D、E、B、F为顶点的四边形可以是矩形,理由如下:
∵E从A出发以1cm/s的速度向C运动,F从C出发以acm/s的速度向A运动,且F比E晚2秒钟,
∴EF=BD=10-t+10-(t-2)a=12,①
∴OE=OF=10-t=10-(t-2)a,②
由①②可得a=2,t=4,
∴当a=2,t=4时当E与F相遇前,以D、E、B、F为顶点的四边形是矩形.
点评 此题考查了平行四边形的判定与性质以及矩形的判定,正确应用矩形的判定方法得出EF=BD是解题关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
20.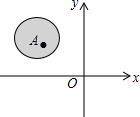 如图,点A在平面直角坐标系中的位置被阴影部分覆盖了,则点A的坐标可能为( )
如图,点A在平面直角坐标系中的位置被阴影部分覆盖了,则点A的坐标可能为( )
 如图,点A在平面直角坐标系中的位置被阴影部分覆盖了,则点A的坐标可能为( )
如图,点A在平面直角坐标系中的位置被阴影部分覆盖了,则点A的坐标可能为( )| A. | (3,2) | B. | (-4,3) | C. | (-2,-3) | D. | (3,-2) |
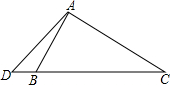 已知,如图,在△ABC中,∠BAC≠90°,∠ABC=2∠C,AD⊥AC,交BC或CB的延长线于D,试说明DC=2AB.
已知,如图,在△ABC中,∠BAC≠90°,∠ABC=2∠C,AD⊥AC,交BC或CB的延长线于D,试说明DC=2AB. 如图,△ABC与△DBC有共同底边BC,且∠BAC=∠BDC,AC交BD于点E,连接AD.求证:∠1=∠2.
如图,△ABC与△DBC有共同底边BC,且∠BAC=∠BDC,AC交BD于点E,连接AD.求证:∠1=∠2. 如图,已知线段AB=6.
如图,已知线段AB=6. 如图,D是△ABC的外角平分线与BA延长线的交点,试判断∠BAC与∠B的大小关系,并说明理由.
如图,D是△ABC的外角平分线与BA延长线的交点,试判断∠BAC与∠B的大小关系,并说明理由.