题目内容
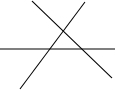 如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.
如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.| A、1 | B、2 | C、3 | D、4 |
考点:角平分线的性质
专题:
分析:由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
解答: 解:∵△ABC内角平分线的交点到三角形三边的距离相等,
解:∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件;
如图:点P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4个.
故选D.
 解:∵△ABC内角平分线的交点到三角形三边的距离相等,
解:∵△ABC内角平分线的交点到三角形三边的距离相等,∴△ABC内角平分线的交点满足条件;
如图:点P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4个.
故选D.
点评:此题考查了角平分线的性质.此题难度适中,注意掌握角平分线上的点到角两边的距离相等定理的应用,注意数形结合思想的应用,小心别漏解.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
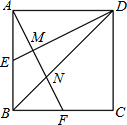 如图,正方形ABCD的边长为2
如图,正方形ABCD的边长为2| 15 |
| A、8 | ||
| B、12 | ||
C、
| ||
| D、15 |
已知关于x的方程x2-4x+5+a•(
+2)=0,若a为正实数,则下列判断正确的是( )
| 1 |
| x |
| A、有三个不等实数根 |
| B、有两个不等实数根 |
| C、有一个实数根 |
| D、无实数根 |
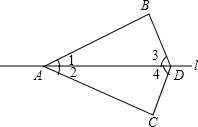 如图,A、D是直线l上两点,B、C两点位于直线l的两侧,若∠1=∠2,则添加下列哪一个条件后,不能保证△ABD≌△ACD( )
如图,A、D是直线l上两点,B、C两点位于直线l的两侧,若∠1=∠2,则添加下列哪一个条件后,不能保证△ABD≌△ACD( )| A、AB=AC |
| B、∠3=∠4 |
| C、∠B=∠C |
| D、BD=CD |
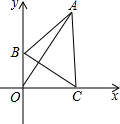 已知在平面直角系xOy中,三角形ABC是边长为a的等边三角形,并且边B点始终在y轴上,点C终在x轴上,则OA的最大值是
已知在平面直角系xOy中,三角形ABC是边长为a的等边三角形,并且边B点始终在y轴上,点C终在x轴上,则OA的最大值是 如图,△ACB中∠ACB=90°,∠A=40°.将△ACB绕点C顺时针旋转得到△DCE,边DE恰好经过点B,则∠DCB的度数为
如图,△ACB中∠ACB=90°,∠A=40°.将△ACB绕点C顺时针旋转得到△DCE,边DE恰好经过点B,则∠DCB的度数为