题目内容
国际象棋比赛的奖金总数为10000元,发给前五名.每一名的奖金都不一样,名次在前的钱数要比名次在后的钱数多.每份奖金钱数都是100元的整数倍.现在规定,第一名的钱数是第二、第三名两人之和,第二名的钱数是第四、第五名两人之和,那么第三名最多能得多少元?
考点:奇数与偶数
专题:
分析:设前5名的奖金数为第一名a(百元),第二名b(百元),第三名c(百元),第四名d(百元),第五名e(百元).且a>b>c>d>e(都为整数),依题意,得:①a+b+c+d+e=100;②a=b+c;③b=d+e,再根据以上等式变形,得出b与c的关系式,根据不等式求字母b的范围,在范围内求c的最大整数值.
解答:解:设前5名的奖金数为第一名a,第二名b,第三名c,第四名d,第五名e.
依题意,得:①a+b+c+d+e=100;②a=b+c;③b=d+e,
把②、③代入①得:3b+2c=100,即c=
,
∵b>c,∴b>
,解得b>20,
由c=
,可知b为偶数,当b最小时,c最大,
当b>20时,b的最小整数值是22,
故c的最大值为
=17,
17×100=1700.也就是第三名最多能得1700元.
答:第三名最多能得1700元.
依题意,得:①a+b+c+d+e=100;②a=b+c;③b=d+e,
把②、③代入①得:3b+2c=100,即c=
| 100-3b |
| 2 |
∵b>c,∴b>
| 100-3b |
| 2 |
由c=
| 100-3b |
| 2 |
当b>20时,b的最小整数值是22,
故c的最大值为
| 100-3×22 |
| 2 |
17×100=1700.也就是第三名最多能得1700元.
答:第三名最多能得1700元.
点评:本题考查了奇数与偶数.关键是设出各名次所得的奖金的未知数,根据他们之间的数量关系列出等式,然后依次代换,一步步求解.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
方程|x|-
=
的实数根的个数为( )
| 4 |
| |x| |
| 3|x| |
| x |
| A、1 | B、2 | C、3 | D、4 |
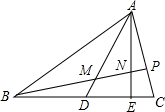 如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )
如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )| A、3:2:1 |
| B、5:3:1 |
| C、25:12:5 |
| D、51:24:10 |
若实数x、y满足(x+y)2+(x+y)-2=0,则x+y的值为( )
| A、1 | B、-2或1 |
| C、2或-1 | D、-2 |
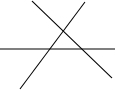 如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.
如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.