题目内容
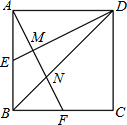 如图,正方形ABCD的边长为2
如图,正方形ABCD的边长为2| 15 |
| A、8 | ||
| B、12 | ||
C、
| ||
| D、15 |
考点:平行线分线段成比例,正方形的性质
专题:计算题
分析:根据正方形的性质以及中点的定义得到AD=AB=2
,AE=BF=
,利用勾股定理计算出DE=AF=5
,易证得△ADE≌△BAF,得到∠ADE=∠BAF,则有∠ADM+∠DAM=90°,利用面积相等得到AM•DE=AE•AD,可到AM=2
,再根据勾股定理计算DM=4
,由AD∥CB,根据平行线分线段成比例定理得到AN:NF=AD:BF=2:1,于是AN=
AF=
,然后利用S△DMN=S△AND-S△AMD进行计算即可.
| 15 |
| 15 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
10
| ||
| 3 |
解答:解:∵正方形ABCD的边长为2
,E,F分别是AB,BC的中点,
∴AD=AB=2
,AE=BF=
,
∴DE=AF=
=5
,
在△ADE和△BAF中
,
∴△ADE≌△BAF(SAS),
∴∠ADE=∠BAF,
而∠BAF+∠DAM=90°,
∴∠ADM+∠DAM=90°,
∴AM•DE=AE•AD,即AM×5
=
×2
,
∴AM=2
,
∴DM=
=4
,
∵AD∥CB,
∴AN:NF=AD:BF=2:1,
∴AN=
AF=
,
∴S△DMN=S△AND-S△AMD=
×4
×
-
×4
×2
=8.
故选A.
| 15 |
∴AD=AB=2
| 15 |
| 15 |
∴DE=AF=
(2
|
| 3 |
在△ADE和△BAF中
|
∴△ADE≌△BAF(SAS),
∴∠ADE=∠BAF,
而∠BAF+∠DAM=90°,
∴∠ADM+∠DAM=90°,
∴AM•DE=AE•AD,即AM×5
| 3 |
| 15 |
| 15 |
∴AM=2
| 3 |
∴DM=
| AD2-AM2 |
| 3 |
∵AD∥CB,
∴AN:NF=AD:BF=2:1,
∴AN=
| 2 |
| 3 |
10
| ||
| 3 |
∴S△DMN=S△AND-S△AMD=
| 1 |
| 2 |
| 3 |
10
| ||
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
故选A.
点评:本题考查了平行线分线段成比例定理:两条直线被一组平行线所截,截得的线段对应成比例.也考查了正方形的性质以及勾股定理.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
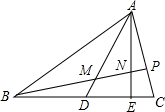 如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )
如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )| A、3:2:1 |
| B、5:3:1 |
| C、25:12:5 |
| D、51:24:10 |
若实数x、y满足(x+y)2+(x+y)-2=0,则x+y的值为( )
| A、1 | B、-2或1 |
| C、2或-1 | D、-2 |
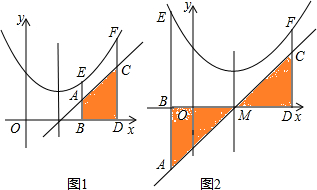 已知点E(x1,y1)、F(x2,y2)为抛物线y=ax2+bx+c上的两点,过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积.
已知点E(x1,y1)、F(x2,y2)为抛物线y=ax2+bx+c上的两点,过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积.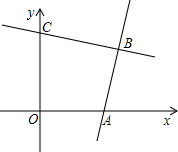 已知:如图,直线y1=mx-3m与x轴交于点A,直线y2=kx+b与y轴交于点C,两直线交于点B.
已知:如图,直线y1=mx-3m与x轴交于点A,直线y2=kx+b与y轴交于点C,两直线交于点B.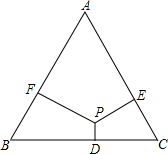 如图,△ABC是边长为12的等边三角形,点P是三角形内的一点,过P分别作边BC,CA,AB的垂线,垂足分别为D,E,F.已知PD:PE:PF=1:2:3,那么四边形BDPF的面积是
如图,△ABC是边长为12的等边三角形,点P是三角形内的一点,过P分别作边BC,CA,AB的垂线,垂足分别为D,E,F.已知PD:PE:PF=1:2:3,那么四边形BDPF的面积是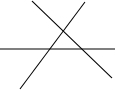 如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.
如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.