题目内容
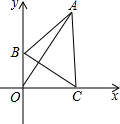 已知在平面直角系xOy中,三角形ABC是边长为a的等边三角形,并且边B点始终在y轴上,点C终在x轴上,则OA的最大值是
已知在平面直角系xOy中,三角形ABC是边长为a的等边三角形,并且边B点始终在y轴上,点C终在x轴上,则OA的最大值是考点:直角三角形斜边上的中线,等边三角形的性质
专题:
分析:取BC的中点D,连接OD、AD,根据直角三角形斜边上的中线等于斜边的一半求出OD的长度,再根据等边三角形的性质可以求出AD的长度,然后根据三角形任意两边之和大于第三边可得点O、D、A三点共线时,OA的长度最大,然后计算即可得解.
解答: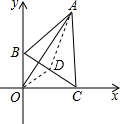 解:如图,取BC的中点D,连接OD、AD,
解:如图,取BC的中点D,连接OD、AD,
则OD=
BC=
a,
AD=
a,
在△OAD中,OD+AD>OA,
所以,当点O、D、A三点共线时,OA的长度最大,
最大值为
a+
a=
a.
故答案为:
a.
 解:如图,取BC的中点D,连接OD、AD,
解:如图,取BC的中点D,连接OD、AD,则OD=
| 1 |
| 2 |
| 1 |
| 2 |
AD=
| ||
| 2 |
在△OAD中,OD+AD>OA,
所以,当点O、D、A三点共线时,OA的长度最大,
最大值为
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等边三角形的性质,以及三角形的三边关系,作出辅助线构造出三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
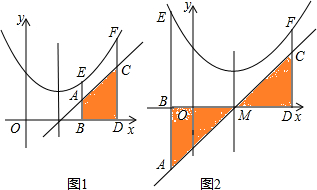 已知点E(x1,y1)、F(x2,y2)为抛物线y=ax2+bx+c上的两点,过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积.
已知点E(x1,y1)、F(x2,y2)为抛物线y=ax2+bx+c上的两点,过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积.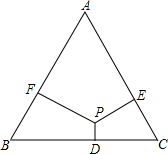 如图,△ABC是边长为12的等边三角形,点P是三角形内的一点,过P分别作边BC,CA,AB的垂线,垂足分别为D,E,F.已知PD:PE:PF=1:2:3,那么四边形BDPF的面积是
如图,△ABC是边长为12的等边三角形,点P是三角形内的一点,过P分别作边BC,CA,AB的垂线,垂足分别为D,E,F.已知PD:PE:PF=1:2:3,那么四边形BDPF的面积是 如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.
如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处. 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,sin∠ABO=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,sin∠ABO=