题目内容
分式
的最小值是 .
| 3x2+6x+5 | ||
|
考点:二次函数的最值
专题:
分析:令分式y=
=6-
,问题转化为考虑函数z=x2+2x+2的最小值,然后用配方法即可求解.
| 3x2+6x+5 | ||
|
| 2 |
| x2+2x+2 |
解答:解:令y=
=6-
,
问题转化为考虑函数z=x2+2x+2的最小值,
∵z=x2+2x+2=(x+1)2+1
∴当x=-1时,zmin=1,
∴ymin=6-2=4,
即分式分式
的最小值是:4.
故答案为:4.
| 3x2+6x+5 | ||
|
| 2 |
| x2+2x+2 |
问题转化为考虑函数z=x2+2x+2的最小值,
∵z=x2+2x+2=(x+1)2+1
∴当x=-1时,zmin=1,
∴ymin=6-2=4,
即分式分式
| 3x2+6x+5 | ||
|
故答案为:4.
点评:本题考查了二次函数的最值及分式的化简求值,难度一般,关键是把分式化简后转化为求函数z=x2+2x+2的最小值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若实数x、y满足(x+y)2+(x+y)-2=0,则x+y的值为( )
| A、1 | B、-2或1 |
| C、2或-1 | D、-2 |
太阳的光线是( )
| A、平行的 |
| B、由一点发出的 |
| C、不平行的 |
| D、向四面八方发散的 |
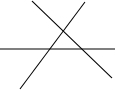 如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.
如图,为了促进当地旅游发展,某地在三条公路周边修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.
 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,sin∠ABO=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,sin∠ABO=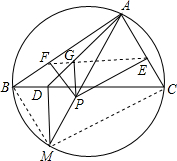 如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.
如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.