题目内容
19.m为正整数,已知二元一次方程组$\left\{\begin{array}{l}{mx+2y=10}\\{3x-2y=0}\end{array}\right.$有整数解,则m2的值为( )| A. | 4 | B. | 49 | C. | 4或49 | D. | 1或49 |
分析 先解方程组,由条件方程组的解为整数,再讨论即可求得m的值,进一步计算m2即可.
解答 解:解方程组$\left\{\begin{array}{l}{mx+2y=10}\\{3x-2y=0}\end{array}\right.$可得$\left\{\begin{array}{l}{x=\frac{10}{m+3}}\\{y=\frac{15}{m+3}}\end{array}\right.$,
∵方程组$\left\{\begin{array}{l}{mx+2y=10}\\{3x-2y=0}\end{array}\right.$有整数解,
∴m+3为10和15的公约数,且m为正整数,
∴m+3=5,解得m=2,
∴m2=4,
故选A.
点评 本题主要考查二元一次方程组的解,求出方程组的解得出m满足的条件是解题的关键.

练习册系列答案
相关题目
14.近年来,全国房价不断上涨,某市201 4年4月份的房价平均每平方米为6600元,比2012年同期的房价平均每平方米上涨了2000元,假设这两年该市房价的平均增长率均为x,则关于x的方程为( )
| A. | (1+x)2=2000 | B. | 2000(1+x)2=6600 | ||
| C. | (6600-200)(1+x)=6600 | D. | (6600-2000)(1+x)2=6600 |
8.甲、乙两个工程队各自维修2800米的路面,甲工程队每小时维修路面的速度是乙工程队每小时维修路面速度的4倍,结果甲比乙早2小时完成了任务.设乙工程队每小时维修路面x米,则下面所列方程正确的是( )
| A. | $\frac{2800}{x}$-$\frac{2800}{5x}$=2 | B. | $\frac{2800}{5x}$-$\frac{2800}{x}$=2 | C. | $\frac{2800}{x}$-$\frac{2800}{4x}$=2 | D. | $\frac{2800}{4x}$-$\frac{2800}{x}$=2 |
9.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的.某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分,每立方米仍按a元收费,超过的部分,每立方米按c元收费,该市某户今年四五月份的用水量和所交水费如下表所示:涉牧户每月用水量x立方厘米,应交水费y元.
为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段达到节约用水的目的.某市规定如下用水收费标准:每户每月的用水不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费.该市某户今年4,5月份的用水量和水费如下表所示:
设某户该月用水量为x(立方米),应交水费y(元).
(1)求a,c的值;
(2)当x≤6,x≥6时,分别写出y于x的函数关系式;
(3)若该户6月份的用水量为8立方米,求该户6月份的水费是多少元?
为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段达到节约用水的目的.某市规定如下用水收费标准:每户每月的用水不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费.该市某户今年4,5月份的用水量和水费如下表所示:
| 月份 | 用水量(m3) | 收费(元) |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
(1)求a,c的值;
(2)当x≤6,x≥6时,分别写出y于x的函数关系式;
(3)若该户6月份的用水量为8立方米,求该户6月份的水费是多少元?
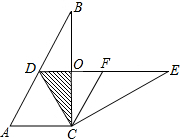 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,DE交BC于点O.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,DE交BC于点O.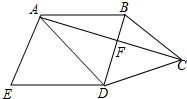 如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.