题目内容
18.竖直上抛物体的高度h和时间t符合关系式h=v0t-$\frac{1}{2}$gt2,其中重力加速度g以10米/秒2计算.爆竹点燃后以初速度v0=20米/秒上升,问经过多少时间爆竹离地15米?分析 根据题意,可以将h=15代入题目中的关系式h=v0t-$\frac{1}{2}$gt2,从而可以求得t的值,本题得以解决.
解答 解:由题意可得,
将h=15代入h=v0t-$\frac{1}{2}$gt2,得
15=10t-$\frac{1}{2}×10×{t}^{2}$,
解得,t1=1,t2=3,
答:经过1秒或3秒时,爆竹离地15米.
点评 本题考查一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件,会求一元二次方程的解,注意此题最后要写上答.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
19.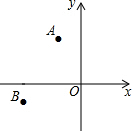 如图,在平面直角坐标系中,已知点A(-4,8),B(-10,-3),以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-4,8),B(-10,-3),以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABO缩小,则点A的对应点A′的坐标是( )
 如图,在平面直角坐标系中,已知点A(-4,8),B(-10,-3),以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-4,8),B(-10,-3),以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABO缩小,则点A的对应点A′的坐标是( )| A. | (-2,4) | B. | (-8,16) | C. | (-2,4)或(2,-4) | D. | (-8,16)或(8,-16) |
10.麓山组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为100元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)假设售价与销售量始终满足(1)中所求函数关系,若商场计划每天的销售利润为3500元,则其单价应定为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售价x(元/双) | 150 | 200 | 250 | 300 |
| 销售量y(双) | 40 | 30 | 24 | 20 |
(2)假设售价与销售量始终满足(1)中所求函数关系,若商场计划每天的销售利润为3500元,则其单价应定为多少元?
7.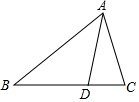 如图,D是△ABC的边BC上任一点,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面积为a,则△ACD的面积为( )
如图,D是△ABC的边BC上任一点,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面积为a,则△ACD的面积为( )
 如图,D是△ABC的边BC上任一点,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面积为a,则△ACD的面积为( )
如图,D是△ABC的边BC上任一点,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面积为a,则△ACD的面积为( )| A. | a | B. | $\frac{1}{2}a$ | C. | $\frac{1}{3}a$ | D. | $\frac{1}{4}$a |
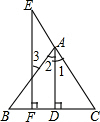 如图:已知:AD⊥BC于D,EF⊥BC于F,∠E=∠3,∠1与∠2相等吗?试说明理由.
如图:已知:AD⊥BC于D,EF⊥BC于F,∠E=∠3,∠1与∠2相等吗?试说明理由. 如图,在Rt△ABC中,∠B=90°,DE⊥AC,DE=3,AE=4,CE=6,则BC的长度为6.
如图,在Rt△ABC中,∠B=90°,DE⊥AC,DE=3,AE=4,CE=6,则BC的长度为6.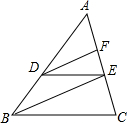 如图,在△ABC中,D是AB 上一点,且$\frac{AD}{DB}$=$\frac{3}{2}$,E、F是AC上的点,且DE∥BC,DF∥BE,AF=9.求EC的长.
如图,在△ABC中,D是AB 上一点,且$\frac{AD}{DB}$=$\frac{3}{2}$,E、F是AC上的点,且DE∥BC,DF∥BE,AF=9.求EC的长.