题目内容
7．
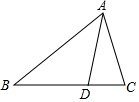如图，D是△ABC的边BC上任一点，已知AB=6，AD=3，∠DAC=∠B．若△ABD的面积为a，则△ACD的面积为（ ）| A． | a | B． | $\frac{1}{2}a$ | C． | $\frac{1}{3}a$ | D． | $\frac{1}{4}$a |
分析 首先证明△ACD∽△BCA，由相似三角形的性质可得：△ACD的面积：△ABC的面积为1：4，因为△ABD的面积为a，进而求出△ACD的面积．
解答 解：∵∠DAC=∠B，∠C=∠C，
∴△ACD∽△BCA，
∵AB=6，AD=3，
∴△ACD的面积：△ABC的面积为1：4，
∴△ACD的面积：△ABD的面积=1：3，
∵△ABD的面积为a，
∴△ACD的面积为$\frac{1}{3}$a，
故选C．
点评 本题考查了相似三角形的判定和性质：相似三角形的面积比等于相似比的平方，证明三角形相似是解决问题的突破口．
练习册系列答案
阅读快车系列答案
相关题目
如图，有一堆土，甲处比乙处高50cm，现在要把这堆土推平整，使甲处和乙处一样高，要从甲处取多少厘米厚的土填在乙处？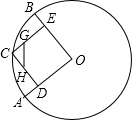
在⊙O中，半径OA、OB互相垂直，点C为弧$\widehat{AB}$上一点（不与A、B重合），CD⊥OA，CE⊥OB，垂足分别为D、E，点G、H分别在CE、CD上，且CG=$\frac{1}{3}$CE，CH=$\frac{1}{3}$CD，当C点在弧$\widehat{AB}$上顺时针运动时，已知⊙O的半径长为6，则GH的长度为（ ）