题目内容
9.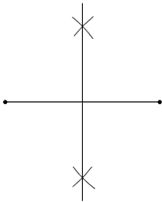 如图所示的尺规作图的痕迹表示的是( )
如图所示的尺规作图的痕迹表示的是( )| A. | 尺规作线段的垂直平分线 | B. | 尺规作一条线段等于已知线段 | ||
| C. | 尺规作一个角等于已知角 | D. | 尺规作角的平分线 |
分析 利用线段垂直平分线的作法进而判断得出答案.
解答 解:如图所示:可得尺规作图的痕迹表示的是尺规作线段的垂直平分线.
故选:A.
点评 此题主要考查了基本作图,正确把握作图方法是解题关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
4.宁波奉化水蜜桃被推为名桃之首,驰名中外,某水蜜桃种植基地欲将n吨水蜜桃运往A,B,C三地销售,要求:①运往各地的质量为整数吨;②运往C地的质量是运往A地质量的两倍.设安排x吨水蜜桃运往A地.
(1)当n=20时:
①根据表中信息填表,并求出运往B地每吨水蜜桃的费用.
②若运往B地的水蜜桃质量不多于运往A地的质量,总运费不超过5520元,则具体有哪几种运输方案?
(2)若总运费为7360元,求n的最小值.
(1)当n=20时:
①根据表中信息填表,并求出运往B地每吨水蜜桃的费用.
| A地 | B地 | C地 | 合计 | |
| 水蜜桃质量(吨) | x | 20-3x | 2x | 20 |
| 运费(元) | 300x | 80(20-3x) | 500x | 560x+1600 |
(2)若总运费为7360元,求n的最小值.
18.在下列二次根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{2a}$ | B. | $\sqrt{4}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
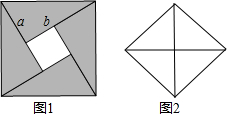 问题情境:
问题情境: