题目内容
4.宁波奉化水蜜桃被推为名桃之首,驰名中外,某水蜜桃种植基地欲将n吨水蜜桃运往A,B,C三地销售,要求:①运往各地的质量为整数吨;②运往C地的质量是运往A地质量的两倍.设安排x吨水蜜桃运往A地.(1)当n=20时:
①根据表中信息填表,并求出运往B地每吨水蜜桃的费用.
| A地 | B地 | C地 | 合计 | |
| 水蜜桃质量(吨) | x | 20-3x | 2x | 20 |
| 运费(元) | 300x | 80(20-3x) | 500x | 560x+1600 |
(2)若总运费为7360元,求n的最小值.
分析 (1)①根据运往B地的产品吨数=总吨数-运往A地的产品吨数-运往C地的产品吨数;B地运费=总运费-A地运费-C地运费,即可补全图表;
②根据运往B地的吨数不多于运往A地的吨数,总运费不超过5520元列出不等式组,求出x的取值范围,再根据x只能取整数,即可得出运输方案;
(2)总运费=A产品的运费+B产品的运费+C产品的运费,进而根据函数的增减性再求出x的范围即可求出n的最小值.
解答 解:(1)①运往C地的产品吨数=2x,运往B地的产品吨数=总吨数-运往A地的产品吨数-运往C地的产品吨数=(20-3x)吨.
B地运费=总运费-A地运费-C地运费=560x+1600-800x=80(20-3x).
故答案分别为20-3x,2x,80(20-3x).
②由题意得$\left\{\begin{array}{l}{20-3x≤x}\\{560x+1600≤5520}\end{array}\right.$,解得5≤x≤7,
∵x是整数,
∴x=5或6或7.x=7不合题意舍弃
有两种方案,分别是(i)A地5吨,B地5吨,C地10吨;(ii)A地6吨,B地2吨,C地12吨;
(2)由题意:300x+80(n-3x)+500x=7360,
整理得7x+n=92,
∴n=92-7x,
∵n-3x>0,
∴92-7x-3x>0,
∴x<9.2,
∵x是整数,
∴x=9时,n最小值=92-63=29.
点评 考查一元一次不等式组的应用,解题的关键是理解题意,认真读懂表格信息,难点是运费条件在表格中得到,第二个问题中自变量x的范围的确定也是难点,属于中考常考题型.

练习册系列答案
相关题目
15. 按如图方式折叠一张对边互相平行的纸条,EF是折痕,若∠EFB=32°,则
按如图方式折叠一张对边互相平行的纸条,EF是折痕,若∠EFB=32°,则
(1)∠C′EF=32°(2)∠AEC=148°(3)∠BGE=64°(4)∠BFD=116°.
以上结论正确的是( )
 按如图方式折叠一张对边互相平行的纸条,EF是折痕,若∠EFB=32°,则
按如图方式折叠一张对边互相平行的纸条,EF是折痕,若∠EFB=32°,则(1)∠C′EF=32°(2)∠AEC=148°(3)∠BGE=64°(4)∠BFD=116°.
以上结论正确的是( )
| A. | ①③ | B. | ②④ | C. | ①③④ | D. | ②③④ |
12. 我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
(1)A点与B或C两点的经度差为$\frac{10}{3}$(单位:度).
(2)通过测量发现,∠BAC=95°,∠BCA=30°,已知北纬31°00′(即点A所在的纬度)处两条相差1°的经线之间的实际距离为96km.我空军一架巡逻机在该区域执行巡逻任务,飞行速度为30km/min,求飞机沿东经125°经线方向从B点飞往C点大约需要多少时间.(已知tan35°=0.7,tan55°=$\frac{10}{7}$,结果保留整数)
 我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:| A | B | C | |
| 北纬(度) | 31°00′ | 33°11′ | 25°38′ |
| 东经(度) | 128°20′ | 125°00′ | 125°00′ |
(2)通过测量发现,∠BAC=95°,∠BCA=30°,已知北纬31°00′(即点A所在的纬度)处两条相差1°的经线之间的实际距离为96km.我空军一架巡逻机在该区域执行巡逻任务,飞行速度为30km/min,求飞机沿东经125°经线方向从B点飞往C点大约需要多少时间.(已知tan35°=0.7,tan55°=$\frac{10}{7}$,结果保留整数)
9.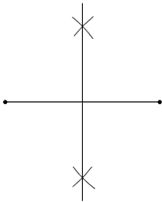 如图所示的尺规作图的痕迹表示的是( )
如图所示的尺规作图的痕迹表示的是( )
 如图所示的尺规作图的痕迹表示的是( )
如图所示的尺规作图的痕迹表示的是( )| A. | 尺规作线段的垂直平分线 | B. | 尺规作一条线段等于已知线段 | ||
| C. | 尺规作一个角等于已知角 | D. | 尺规作角的平分线 |
16.已知正比例函数y=(m-3)x的图象过第二、四象限,则m的取值范围是( )
| A. | m≥3 | B. | m>3 | C. | m≤3 | D. | m<3 |
 利用一面墙(墙的长度为24m),另三边用用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.
利用一面墙(墙的长度为24m),另三边用用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.