题目内容
17.解下列一元二次方程①x2-6x+4=0
②2x2-4x+1=0.
分析 ①方程整理后,利用配方法求出解即可;
②方程整理后,利用配方法求出解即可.
解答 解:①方程整理得:x2-6x=-4,
配方得:x2-6x+9=5,即(x-3)2=5,
开方得:x-3=±$\sqrt{5}$,
解得:x1=3+$\sqrt{5}$,x2=3-$\sqrt{5}$;
②方程整理得:x2-2x=-$\frac{1}{2}$,
配方得:x2-2x+1=$\frac{1}{2}$,即(x-1)2=$\frac{1}{2}$,
开方得:x-1=±$\frac{\sqrt{2}}{2}$,
解得:x1=1+$\frac{\sqrt{2}}{2}$,x2=1-$\frac{\sqrt{2}}{2}$.
点评 此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
8.下列说法正确的是( )
| A. | 相等的角是对顶角 | |
| B. | 同旁内角相等,两直线平行 | |
| C. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 | |
| D. | 经过直线外一点,有且只有一条直线与这条直线平行 |
5.平面直角坐标系中,正六边形ABCDEF的起始位置如图1所示,边AB在x轴上,现将正六边形沿x轴正方向无滑动滚动,第一次滚动后,边BC落在x轴上(如图2);第二次滚动后,边CD落在x轴上,如此继续下去.则第2016次滚动后,落在x轴上的是( )


| A. | 边DE | B. | 边EF | C. | 边FA | D. | 边AB |
12. 我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
(1)A点与B或C两点的经度差为$\frac{10}{3}$(单位:度).
(2)通过测量发现,∠BAC=95°,∠BCA=30°,已知北纬31°00′(即点A所在的纬度)处两条相差1°的经线之间的实际距离为96km.我空军一架巡逻机在该区域执行巡逻任务,飞行速度为30km/min,求飞机沿东经125°经线方向从B点飞往C点大约需要多少时间.(已知tan35°=0.7,tan55°=$\frac{10}{7}$,结果保留整数)
 我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:| A | B | C | |
| 北纬(度) | 31°00′ | 33°11′ | 25°38′ |
| 东经(度) | 128°20′ | 125°00′ | 125°00′ |
(2)通过测量发现,∠BAC=95°,∠BCA=30°,已知北纬31°00′(即点A所在的纬度)处两条相差1°的经线之间的实际距离为96km.我空军一架巡逻机在该区域执行巡逻任务,飞行速度为30km/min,求飞机沿东经125°经线方向从B点飞往C点大约需要多少时间.(已知tan35°=0.7,tan55°=$\frac{10}{7}$,结果保留整数)
9.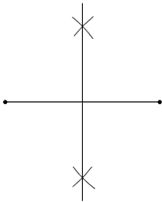 如图所示的尺规作图的痕迹表示的是( )
如图所示的尺规作图的痕迹表示的是( )
 如图所示的尺规作图的痕迹表示的是( )
如图所示的尺规作图的痕迹表示的是( )| A. | 尺规作线段的垂直平分线 | B. | 尺规作一条线段等于已知线段 | ||
| C. | 尺规作一个角等于已知角 | D. | 尺规作角的平分线 |
3.用半径为12cm,圆心角为150°的扇形做一个圆锥模型的侧面,则此圆锥底面圆的半径为( )
| A. | 5cm | B. | 30cm | C. | 6cm | D. | 10cm |
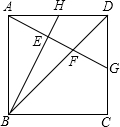 如图,正方形ABCD,H为AD中点,AG⊥BH分别交BH、BD、CD于E、F、G.
如图,正方形ABCD,H为AD中点,AG⊥BH分别交BH、BD、CD于E、F、G.