题目内容
16.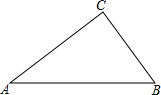 如图,在Rt△ABC中,∠C=90°.
如图,在Rt△ABC中,∠C=90°.(1)用直尺和圆规分别作∠A和∠B的平分线,相交于点O(保留作图痕迹,不写作法);
(2)求∠AOB度数;
(3)如果AC=4cm,BC=3cm.试求出点O到AB的距离.
分析 (1)利用角平分线的作法得出其交点O即可;
(2)利用角平分线的性质结合三角形内角和定理得出答案;
(3)利用三角形内心的性质结合直角三角形内切圆半径求法得出答案.
解答  解:(1)如图所示:点O即为所求;
解:(1)如图所示:点O即为所求;
(2)∵∠C=90°,作∠A和∠B的平分线,相交于点O,
∴∠OAB+∠OBA=45°,
∴∠AOB=135°;
(3)∵AC=4cm,BC=3cm,∠C=90°,
∴AB=5cm,
∴Rt△ABC内切圆半径为:$\frac{3+4-5}{2}$=1(cm),
则点O到AB的距离为1cm.
点评 此题主要考查了复杂作图以及三角形内角和定理、三角形内心的性质,正确把握三角形内心的性质是解题关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
8.已知△ABC中,AB=AC,D是BC的中点,那么下列说法不正确的是( )
| A. | AD是底边上的中线 | B. | AD是底边上的高 | ||
| C. | AD是顶角的平分线 | D. | AD是一腰上的中线 |
6.不改变原式的值,将式子12-(+3)-(-4)+(-6)中的减法改成加法并省略括号、加号,则正确的结果是( )
| A. | -12-3+4-6 | B. | 12-3-4-6 | C. | 12-3+4-6 | D. | 12+3-4-6 |
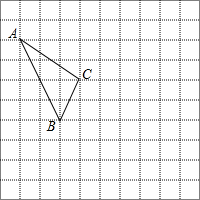 如图,在正方形网格中,每个小正方形的边长为1,格点△ABC的顶点A、C的坐标分别为(-4,5)、(-1,3)
如图,在正方形网格中,每个小正方形的边长为1,格点△ABC的顶点A、C的坐标分别为(-4,5)、(-1,3)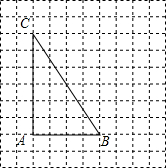 利用网格线画图:如图,点A、B、C都在正方形网格的格点上.
利用网格线画图:如图,点A、B、C都在正方形网格的格点上.