题目内容
11.已知△ABC的三边a、b、c满足$\sqrt{a-1}$+|b-1|+(c-$\sqrt{2}$)2=0,则∠B=45°.分析 根据给出的条件求出三角形的三边长,再根据勾股定理的逆定理来判定三角形的形状.
解答 解:∵$\sqrt{a-1}$+|b-1|+(c-$\sqrt{2}$)2=0,
∴a=1,b=1,c=$\sqrt{2}$,
∵12+12=$\sqrt{2}$2,
∴△ABC是等腰直角三角形,
所以∠B=45°,
故答案为:45
点评 本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | ($\frac{2{a}^{-3}b}{-{c}^{3}}$)2=$\frac{4{a}^{9}b}{{c}^{5}}$ | B. | ($\frac{2x-y}{-5{a}^{2}}$)2=$\frac{4{x}^{2}-{y}^{2}}{25{a}^{4}}$ | ||
| C. | (3xny-n)-m=$\frac{{y}^{mn}}{{3}^{m}x^{mn}}$ | D. | (-$\frac{{b}^{2}}{a}$)2n=-$\frac{{b}^{2+2n}}{{a}^{n}}$ |
19.下列各式去括号正确的是( )
| A. | -(a+b)=a-b | B. | 2(x-2)=2x-2 | C. | -3(2x-1)=-6x-3 | D. | 2-(-x+3)×2=2+2x-6 |
6.在$\frac{\sqrt{2}}{2}$,$\frac{π}{4}$,1.732,0.3030030003…,$\sqrt{16}$,-$\frac{22}{7}$,$\root{3}{8}$中,无理数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.对于代数式-$\frac{3{a}^{3}{b}^{2}}{4}$,下列结论正确的是( )
| A. | 它的系数是$\frac{3}{4}$,次数是5 | B. | 它的系数是-$\frac{3}{4}$,次数是6 | ||
| C. | 它的系数是$\frac{3}{4}$,次数是6 | D. | 它的系数是-$\frac{3}{4}$,次数是5 |
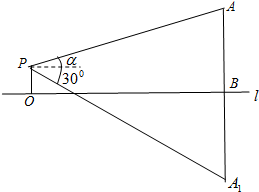 在湖心有一座塔,小明想知道这座塔的高度,于是他在岸边架起了测角仪.他测量得数据如下(如图示):测角仪位置(P)距水平面(l)的距离为1.5米(即OP),测得塔顶A的仰角为α(其中tanα=$\frac{1}{3}$),测得塔顶在水中倒影A1(即AB=A1B)的俯角为300.那么这座塔的高度AB=3+$\frac{3\sqrt{3}}{2}$.(结果保留根号)
在湖心有一座塔,小明想知道这座塔的高度,于是他在岸边架起了测角仪.他测量得数据如下(如图示):测角仪位置(P)距水平面(l)的距离为1.5米(即OP),测得塔顶A的仰角为α(其中tanα=$\frac{1}{3}$),测得塔顶在水中倒影A1(即AB=A1B)的俯角为300.那么这座塔的高度AB=3+$\frac{3\sqrt{3}}{2}$.(结果保留根号)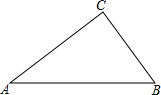 如图,在Rt△ABC中,∠C=90°.
如图,在Rt△ABC中,∠C=90°.