题目内容
14．已知圆柱的全面积为600πcm2，母线长为20cm．（1）求它的底面半径；
（2）画出它的表面展开图．（按1：10的比例）
分析 （1）设它的底面半径为xcm，然后根据全面积为600πcm2列方程求解即可；
（2）圆柱的展开图中包含两个圆面和一个长方形．
解答 解：（1）设它的底面半径为xcm，则它的底面周长为2πxcm．
根据题意得：2πr2+2πr×20=600π．
解得；r1=10，r2=-30（舍去）．
故圆柱的底面半径为10cm．
（2）如图所示：
点评 本题主要考查的是几何体的展开图，根据圆柱体的表面积公式列出关于r的方程是解题的关键．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
4．已知扇形的圆心角为120°，半径为6cm的圆，则扇形的弧长为（ ）
| A． | 3cm | B． | 3πcm | C． | 4cm | D． | 4πcm |
5．
如图是四张全等的矩形纸片拼成的图形，利用图中阴影部分面积的不同表示方法，可以写出关于a、b的恒等式，下列各式正确的为（ ）
如图是四张全等的矩形纸片拼成的图形，利用图中阴影部分面积的不同表示方法，可以写出关于a、b的恒等式，下列各式正确的为（ ）| A． | （a+b）2=（a-b）2+2ab | B． | （a-b）2=（a+b）2-2ab | C． | （a-b）2=a2-2ab+b2 | D． | （a+b）（a-b）=a2-b2 |
9．下列计算正确的是（ ）
| A． | （$\frac{2{a}^{-3}b}{-{c}^{3}}$）2=$\frac{4{a}^{9}b}{{c}^{5}}$ | B． | （$\frac{2x-y}{-5{a}^{2}}$）2=$\frac{4{x}^{2}-{y}^{2}}{25{a}^{4}}$ | ||
| C． | （3xny-n）-m=$\frac{{y}^{mn}}{{3}^{m}x^{mn}}$ | D． | （-$\frac{{b}^{2}}{a}$）2n=-$\frac{{b}^{2+2n}}{{a}^{n}}$ |
如图，一艘巡洋舰从点A出发，沿正南方向航行了半小时到达点B，再沿南偏西60°方向航行了半小时到达点C，此时测得码头D在C的正东方向，该巡洋舰的速度为80海里/时．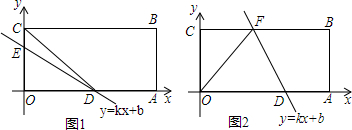
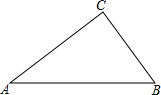如图，在Rt△ABC中，∠C=90°．