题目内容
1.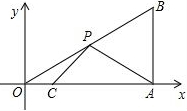 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的纵坐标为2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,点P是斜边DB上的一个动点,则△PAC的周长的最小值为2$\sqrt{7}$+4.
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的纵坐标为2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,点P是斜边DB上的一个动点,则△PAC的周长的最小值为2$\sqrt{7}$+4.【说明:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.】
分析 作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AM,求出AD,求出DN、CN,根据勾股定理求出CD,即可得出答案.
解答 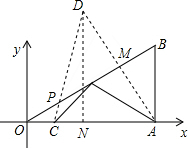 解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,
解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵顶点B的纵坐标为2$\sqrt{3}$,∠B=60°,
∴AB=2$\sqrt{3}$,OA=6,由勾股定理得:OB=4$\sqrt{3}$,
由三角形面积公式得:$\frac{1}{2}$×OA×AB=$\frac{1}{2}$×OB×AM,
∴AM=3,
∴AD=2×3=6,
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴∠NDA=30°,
∴AN=$\frac{1}{2}$AD=3,由勾股定理得:DN=3$\sqrt{3}$,
∵C(1,0),
∴CN=AC-AN=4-3=1,
在Rt△DNC中,由勾股定理得:DC=$\sqrt{{1}^{2}+(3\sqrt{3})^{2}}$=2$\sqrt{7}$,
即PA+PC的最小值是2$\sqrt{7}$,
∴△PAC周长的最小值为:2$\sqrt{7}$+4.
故答案为:2$\sqrt{7}$+4.
点评 本题考查了轴对称-最短路线问题,三角形的内角和定理,勾股定理,含30度角的直角三角形性质的应用,关键是求出P点的位置,题目比较好,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.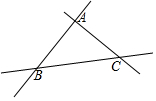 如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )
如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )
 如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )
如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )| A. | △ABC三边的中线的交点上 | B. | △ABC三边垂直平分线的交点上 | ||
| C. | △ABC三条边高的交点上 | D. | △ABC三内角平分线的交点上 |
10.已知xa+a=3是关于x的一元一次方程,则该方程的解为( )
| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=4 |
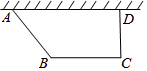 如图,要建造一个直角梯形的花圃,要求AD边靠墙,CD⊥AD,AB:CD=5:4,另外三边的和为20米,设AB的长为5x米
如图,要建造一个直角梯形的花圃,要求AD边靠墙,CD⊥AD,AB:CD=5:4,另外三边的和为20米,设AB的长为5x米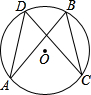 (1)计算:(-$\frac{1}{2}$)-1+$\sqrt{3}$tan30°-sin245°
(1)计算:(-$\frac{1}{2}$)-1+$\sqrt{3}$tan30°-sin245°