题目内容
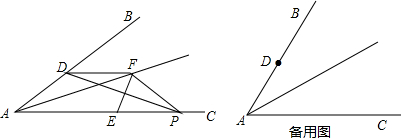
16.已知,如图,点D在射线AB上,且AD=2,点P是射线AC上的一个动点,线段PD的垂直平分线与射线AC交于点E,与∠BAC的平分线交于点F.连结DF、PF、EF.(1)当DF∥AC时,求证:AD=PF.
(2)当∠BAC=60°时,设AP=x,AF=y,求y关于x的函数解析式.
分析 (1)根据角平分线的定义得到∠BAF=∠FAC,由平行线的性质得到∠DAF=∠FAC,等量代换得到∠DAF=∠DFA,由等腰三角形的判定得到AD=DF,由EF垂直平分DP,得到DF=PF,等量代换即可得到结论;
(2)过点F作FG⊥AC于G,FH⊥AB于H,根据角平分线的性质得到FH=FG,由∠BAC=60°,得到∠FAC=30°,根据直角三角形的性质得到FG=$\frac{1}{2}$AF,AG=$\frac{\sqrt{3}}{2}$AF,同理FH=$\frac{1}{2}$AF,AH=$\frac{\sqrt{3}}{2}$AF,由EF垂直平分DP,得到FD=FP,推出Rt△FDH≌Rt△FPG,根据全等三角形的性质得到PG=DH,代入数据即可得到结论.
解答 解:(1)∵AF平分∠BAC,
∴∠BAF=∠FAC,
∵DF∥AC,
∴∠DAF=∠FAC,
∴∠DAF=∠DFA,
∴AD=DF,
∵EF垂直平分DP,
∴DF=PF,
∴AD=PF;
(2)过点F作FG⊥AC于G,FH⊥AB于H,
∵AF平分∠BAC,FG⊥AC,FH⊥AB,
∴FH=FG,∵∠BAC=60°,
∴∠FAC=30°,
∴FG=$\frac{1}{2}$AF,AG=$\frac{\sqrt{3}}{2}$AF,
同理FH=$\frac{1}{2}$AF,AH=$\frac{\sqrt{3}}{2}$AF,
∵EF垂直平分DP,
∴FD=FP,
在Rt△FDH与Rt△FPG中, $\left\{\begin{array}{l}{FD=FP}\\{FH=FG}\end{array}\right.$,
$\left\{\begin{array}{l}{FD=FP}\\{FH=FG}\end{array}\right.$,
∴Rt△FDH≌Rt△FPG,
∴PG=DH,
∵AD=2,AP=x,AF=y,
∴x=$\frac{\sqrt{3}}{2}$y+($\frac{\sqrt{3}}{2}$y-2),
∴y=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$.
点评 本题考查了全等三角形的判定和性质,角平分线的性质,线段垂直平分线的性质,正确的作出辅助线是解题的关键.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
 在Rt△ABC中,∠C=90°,AC=8,BC=6,将其如图折叠使点A与点B重合,折痕为DE,连接BE,则tan∠CBE的值为( )
在Rt△ABC中,∠C=90°,AC=8,BC=6,将其如图折叠使点A与点B重合,折痕为DE,连接BE,则tan∠CBE的值为( )| A. | $\frac{24}{7}$ | B. | $\frac{\sqrt{7}}{3}$ | C. | $\frac{7}{24}$ | D. | $\frac{1}{3}$ |
| A. |  | B. |  | C. |  | D. |  |
 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴于点C和点D,则DC的长为( )
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴于点C和点D,则DC的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |



 如图,在△ABC中,∠C=90°,∠B=60°,AC=6,斜边AB的垂直平分线交AB于点E,交AC于点D,则CD的长为2.
如图,在△ABC中,∠C=90°,∠B=60°,AC=6,斜边AB的垂直平分线交AB于点E,交AC于点D,则CD的长为2.