题目内容
15.计算:①(xy+4)(xy-4)
②$\frac{1}{2}{a^2}b{c^3}•{(-2{a^2}{b^2}c)^2}$
③$\frac{{{{1000}^2}}}{{{{252}^2}-{{248}^2}}}$
④20012
⑤(x+2y-3)(x-2y+3)
⑥(2x-5)(2x+5)-(2x+1)(2x-3)
分析 ①根据平方差公式计算即可;
②先算积的乘方,再算单项式乘以单项式;
③先将分母利用平方差公式计算,再将分子平方,然后相除即可;
④变形为(2000+1)2,再利用完全平方公式计算;
⑤变形为[x+(2y-3)[x-(2y-3)],再根据平方差公式计算;
⑥分别根据平方差公式与多项式乘以多项式的法则计算乘法,再去括号合并同类项即可.
解答 解:①(xy+4)(xy-4)=x2y2-16;
②$\frac{1}{2}{a^2}b{c^3}•{(-2{a^2}{b^2}c)^2}$=$\frac{1}{2}$a2bc3•4a4b4c2=2a6b5c5;
③$\frac{{{{1000}^2}}}{{{{252}^2}-{{248}^2}}}$=$\frac{1000000}{500×4}$=500;
④20012=(2000+1)2=4000000+4000+1=4004001;
⑤(x+2y-3)(x-2y+3)=[x+(2y-3)[x-(2y-3)]=x2-(2y-3)2=x2-4y2+12y-9;
⑥(2x-5)(2x+5)-(2x+1)(2x-3)=4x2-25-(4x2-6x+2x-3)=4x2-25-4x2+6x-2x+3=4x-22.
点评 本题考查了整式的混合运算,掌握运算顺序与运算法则是解题的关键,注意利用公式可使计算简便.

练习册系列答案
相关题目
 如图,AB=5,P是线段AB上的动点,分别以AP、BP为边,在线段AB的同侧作正方形APCD和正方形BPEF,连接CF,则CF的最小值是$\sqrt{5}$.
如图,AB=5,P是线段AB上的动点,分别以AP、BP为边,在线段AB的同侧作正方形APCD和正方形BPEF,连接CF,则CF的最小值是$\sqrt{5}$. 如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形△ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形△DEF;依此作下去…,则第3个三角形的面积等于$\frac{\sqrt{3}{a}^{2}}{64}$.
如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形△ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形△DEF;依此作下去…,则第3个三角形的面积等于$\frac{\sqrt{3}{a}^{2}}{64}$.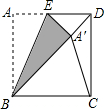 如图,将正方形ABCD沿BE对折,使点A落在对角线BD上A′处,则∠A′CD=22.5°.
如图,将正方形ABCD沿BE对折,使点A落在对角线BD上A′处,则∠A′CD=22.5°.