题目内容
7．已知多项式M=（x-2）（x+2）+（-x+1）（x+3）（1）化简多项式M；
（2）若x满足方程$\frac{2}{x-1}$=$\frac{1}{2x+1}$，求M的值．
分析 （1）多项式M利用平方差公式，多项式乘以多项式法则计算，去括号合并即可得到结果；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验确定出分式方程的解，代入计算即可求出M的值．
解答 解：（1）M=x2-4-x2-2x+3=-2x-1；
（2）分式方程去分母得：4x+2=x-1，
解得：x=-1，
经检验x=-1是分式方程的解，
则M=2-1=1．
点评 此题考查了解分式方程，多项式乘多项式，以及平方差公式，熟练掌握公式及运算法则是解本题的关键．
练习册系列答案
相关题目
如图，一条公路的两边AB∥CD，在AB上有两棵树M，N，在另一边CD上有一棵树P，测得M，N相距50m，∠MPC=30°，∠NPD=75°，则公路的宽度为25m．
如图所示方格纸中每个小正方形的边长为1，其中有三个格点A、B、C，则sin∠ABC=$\frac{9\sqrt{145}}{145}$．
17．
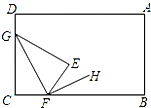如图所示，将一张长方形纸片AB-CD的∠C沿CF折叠（F在BC边上，不与B，C重合），使得C点落在长方形ABCD内部E处，FH平分∠BFE，则∠GFH的度数满足（ ）
如图所示，将一张长方形纸片AB-CD的∠C沿CF折叠（F在BC边上，不与B，C重合），使得C点落在长方形ABCD内部E处，FH平分∠BFE，则∠GFH的度数满足（ ）| A． | ∠GFH＜90° | B． | ∠GFH=90° | C． | ∠GFH＞90° | D． | 0°＜∠GFH＜90° |