题目内容
5．
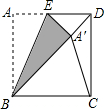如图，将正方形ABCD沿BE对折，使点A落在对角线BD上A′处，则∠A′CD=22.5°．
分析 由四边形ABCD是正方形，可得AB=BC，∠CBD=45°，又由折叠的性质可得：A′B=AB，根据等边对等角与三角形内角和定理，即可求得∠BA′C的度数，然后根据三角形外角的性质即可得到结论．
解答 解：∵四边形ABCD是正方形，
∴AB=BC，∠CBD=45°，
根据折叠的性质可得：A′B=AB，
∴A′B=BC，
∴∠BA′C=∠BCA′=$\frac{180∠CBD}{2}$=$\frac{180°-45°}{2}$=67.5°，
∴∠A′CD=67.5°-45°=22.5°，
故答案为：22.5．
点评 此题考查了折叠的性质与正方形的性质．此题难度不大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．
练习册系列答案
相关题目
如图的螺旋形由一系列含30°的直角三角形组成，其序号依次为①、②、③、④、⑤…，则第6个直角三角形的斜边长为$\frac{9\sqrt{3}}{16}$．
17．
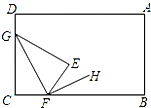如图所示，将一张长方形纸片AB-CD的∠C沿CF折叠（F在BC边上，不与B，C重合），使得C点落在长方形ABCD内部E处，FH平分∠BFE，则∠GFH的度数满足（ ）
如图所示，将一张长方形纸片AB-CD的∠C沿CF折叠（F在BC边上，不与B，C重合），使得C点落在长方形ABCD内部E处，FH平分∠BFE，则∠GFH的度数满足（ ）| A． | ∠GFH＜90° | B． | ∠GFH=90° | C． | ∠GFH＞90° | D． | 0°＜∠GFH＜90° |