题目内容
2. 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF.(1)求证:AC=EF;
(2)求证:四边形ADFE是平行四边形.
分析 (1)根据等边三角形的性质得出∠AEF=$\frac{1}{2}$∠AEB=30°,AE=AB,∠EFA=90°,求出∠AEF=∠BAC,∠EFA=∠ACB,根据AAS推出△AEF≌△BAC即可;
(2)根据等边三角形的性质得出AC=AD,∠DAC=60°,求出AD=EF,再求出AD∥EF,根据平行四边形的判定得出即可.
解答 证明:(1)∵△BAE是等边三角形,EF⊥AB,
∴∠AEF=$\frac{1}{2}$∠AEB=30°,AE=AB,∠EFA=90°,
∵∠ACB=90°,∠BAC=30°,
∴∠AEF=∠BAC,∠EFA=∠ACB,
在△AEF和△BAC中
$\left\{\begin{array}{l}{∠EFA=∠ACB}\\{∠AEF=∠BAC}\\{AE=AB}\end{array}\right.$
∴△AEF≌△BAC,
∴AC=EF;
(2)∵△ACD是等边三角形,
∴AC=AD,∠DAC=60°,
由(1)的结论得AC=EF,
∴AD=EF,
∵∠BAC=30°,
∴∠FAD=∠BAC+∠DAC=90°,
∵∠EFA=90°,
∴AD∥EF,
∵AD=EF,
∴四边形ADFE是平行四边形.
点评 本题考查了平行四边形的性质,等边三角形的性质,全等三角形的性质和判定,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.某商品的进价是500元,标价为750元,商店要求以利润不低于5%的售价打折出售,此商品最低可以打( )
| A. | 6折 | B. | 7折 | C. | 8折 | D. | 9折 |
14.已知两点P1(1,y1),P2(5,y2)在反比例函数y=$\frac{5}{x}$的图象上,下列结论正确的是( )
| A. | 0<y1<y2 | B. | 0<y2<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
 如图,△ABC中,∠A=50°,∠B=70°,CD平分∠ACB,DE交AB于D交AC于E,∠CDE=30°,求∠ADE的度数.
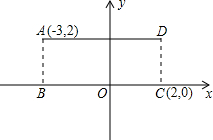
如图,△ABC中,∠A=50°,∠B=70°,CD平分∠ACB,DE交AB于D交AC于E,∠CDE=30°,求∠ADE的度数.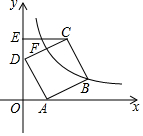 如图,正方形ABCD的两个顶点A,D分别在x轴和y轴上,CE⊥y轴于点E,OA=2,∠ODA=30°.若反比例函数y=$\frac{k}{x}$的图象过CE的中点F,则k的值为2$\sqrt{3}$+6.
如图,正方形ABCD的两个顶点A,D分别在x轴和y轴上,CE⊥y轴于点E,OA=2,∠ODA=30°.若反比例函数y=$\frac{k}{x}$的图象过CE的中点F,则k的值为2$\sqrt{3}$+6. 在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°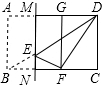 如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上一动点(不与点B、D重合),将矩形沿过点E的直线MN折叠,使得点A、B的对应点G、F分别在直线AD与BC上,当△DEF为直角三角形时,CN的长为$\frac{25}{4}$或$\frac{7}{4}$.
如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上一动点(不与点B、D重合),将矩形沿过点E的直线MN折叠,使得点A、B的对应点G、F分别在直线AD与BC上,当△DEF为直角三角形时,CN的长为$\frac{25}{4}$或$\frac{7}{4}$.