Question

11．已知抛物线y=ax²+bx+c的顶点为（2，5），且与y轴交于点C（0，1）．
（1）求抛物线的表达式；
（2）若-1≤x≤3，试求y的取值范围；
（3）若M（n²-4n+6，y₁）和N（-n²+n+$\frac{7}{4}$，y₂）是抛物线上的不重合的两点，试判断y₁与y₂的大小，并说明理由．

Answer 1

分析 （1）利用抛物线的顶点式求二次函数的解析式；
（2）分别求出当x=-1和x=3时对应的y值，画图象得出y的取值；
（3）先将点M和N两点的横坐标代入抛物线的解析式中求y₁和y₂，根据大于、等于、不于三种情况进行判断即可．

解答 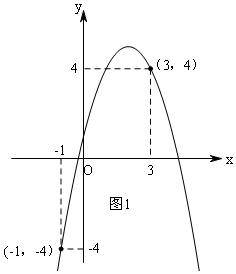解：（1）∵抛物线y=ax²+bx+c的顶点为（2，5），
∴设抛物线的表达式为：y=a（x-2）²+5，
把（0，1）代入得：a（0-2）²+5=1，
a=-1，
∴抛物线的表达式为：y=-（x-2）²+5=-x²+4x+1；
（2）画图象如图1：
当x=-1时，y=-4；
当x=3时，y=4；
由图象得：若-1≤x≤3，y的取值范围是：-4≤y≤5；
（3）当x=n²-4n+6时，y₁=-（n²-4n+6-2）²+5，
y₁=-（n-2）⁴+5，
当x=-n²+n+$\frac{7}{4}$时，y₂=-（-n²+n+$\frac{7}{4}$-2）²+5，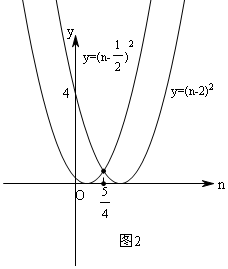
y₂=-（n-$\frac{1}{2}$）⁴+5，
当y₁＞y₂时，-（n-2）⁴+5＞-（n-$\frac{1}{2}$）⁴+5，
（n-2）²＜（n-$\frac{1}{2}$）²，
由（n-2）²=（n-$\frac{1}{2}$）²，解得：n=$\frac{5}{4}$，
如图2，由图象得：当n＞$\frac{5}{4}$时，（n-2）²＜（n-$\frac{1}{2}$）²，
即y₁＞y₂；
同理得：当n＜$\frac{5}{4}$时，（n-2）²＞（n-$\frac{1}{2}$）²，
即y₁＜y₂；
当n=$\frac{5}{4}$时，n²-4n+6≠-n²+n+$\frac{7}{4}$，
（n-2）²=（n-$\frac{1}{2}$）²，
即y₁=y₂．

点评 本题考查了利用待定系数法求抛物线的解析式、二次函数的性质、二次函数的图象，第二问注意利用数形结合的思想，当-1≤x≤3时，y的最大值不是4，而是5；第三问有难度，注意利用二次函数的图象解决问题．