题目内容
7. 在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°(1)求证:GD=GF.
(2)已知BC=10,DF=8$\sqrt{2}$.求CD的长.
分析 (1)由已知条件和平行四边形的性质可证明∠FDG=∠DFG,进而可得GD=GF;
(2)由勾股定理易求GF的长,再证明△EBF≌△ECG,可得GE=4,在 Rt△CGE 中由勾股定理 CG2=CE2-GE2可得CG的长,进而可求出CD的长.
解答 解:
(1)证明:
∵EF⊥AB,
∴∠GFB=90°
∵四边形ABCD是平行四边形,
∴AB∥CD,∠DGF=∠GFB=90°,
在△DGF中,已知∠FDG=45°,
∴∠DFG=45°,
∴∠FDG=∠DFG,
∴GD=GF;
(2)解:由(1)得DG2+GF2=DF2,DF=8$\sqrt{2}$,
∴GF2=64,
∴GF=8,
∵点E 是BC中点,
∵BC=10,
∴CE=5,
∵四边形ABCD是平行四边形,
∴∠GCE=∠EBF
在△EBF和△ECG中,
$\left\{\begin{array}{l}{∠GCE=∠EBF}\\{∠ECG=∠EFB=90°}\\{CE=BE}\end{array}\right.$,
∴△EBF≌△ECG,
∴GE=4,
在 Rt△CGE 中 CG2=CE2-GE2=9,
∴CG=3,
∴CD=8-3=5.
点评 本题考查了平行四边形的性质、全等三角形的判断和性质以及勾股定理的运用,题目的综合性较强,难度中等,熟记平行四边形的各种性质是解题的关键.

练习册系列答案
相关题目
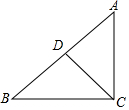 如图,在△ABC中,∠ACB=90°,∠B=35°,CD是AB上的中线,则∠ADC=70°.
如图,在△ABC中,∠ACB=90°,∠B=35°,CD是AB上的中线,则∠ADC=70°.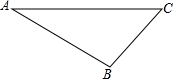 如图,已知△ABC
如图,已知△ABC 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF.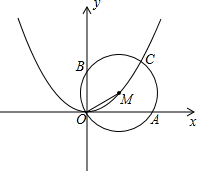 如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$.
如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$.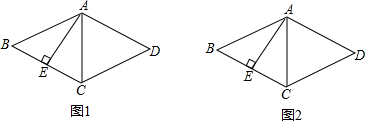
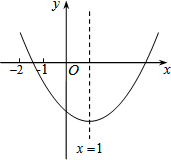 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论: