题目内容
13. 如图,△ABC中,∠A=50°,∠B=70°,CD平分∠ACB,DE交AB于D交AC于E,∠CDE=30°,求∠ADE的度数.
如图,△ABC中,∠A=50°,∠B=70°,CD平分∠ACB,DE交AB于D交AC于E,∠CDE=30°,求∠ADE的度数.
分析 根据三角形的内角和得到∠ACD=60°,根据角平分线的定义得到∠ACD=$\frac{1}{2}$ACB=30°,根据三角形的外角的性质得到∠AED=∠EDC+∠ACD=60°,根据三角形的内角和即可得到结论.
解答 解:∵∠A=50°,∠B=70°,
∴∠ACD=60°,
∵CD平分∠ACB,
∴∠ACD=$\frac{1}{2}$ACB=30°,
∴∠AED=∠EDC+∠ACD=60°,
∴∠ADE=180°-∠A-∠AED=70°,
点评 本题考查了三角形的内角和,角平分线的定义,熟练掌握三角形的内角和是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列说法中,正确的是( )
| A. | 同位角相等 | B. | 矩形的对角线一定互相垂直 | ||
| C. | 对角线相等的四边形是矩形 | D. | 四条边相等的四边形是菱形 |
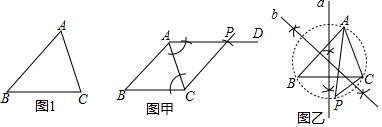
 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF.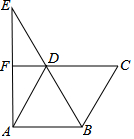 如图,在菱形ABCD中,延长BD到E使得BD=DE,连接AE,延长CD交AE于点F.
如图,在菱形ABCD中,延长BD到E使得BD=DE,连接AE,延长CD交AE于点F.