题目内容
17.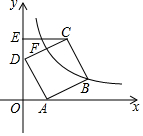 如图,正方形ABCD的两个顶点A,D分别在x轴和y轴上,CE⊥y轴于点E,OA=2,∠ODA=30°.若反比例函数y=$\frac{k}{x}$的图象过CE的中点F,则k的值为2$\sqrt{3}$+6.
如图,正方形ABCD的两个顶点A,D分别在x轴和y轴上,CE⊥y轴于点E,OA=2,∠ODA=30°.若反比例函数y=$\frac{k}{x}$的图象过CE的中点F,则k的值为2$\sqrt{3}$+6.
分析 先根据△CDE≌△DAO,得到DE=AO=2,DO=2$\sqrt{3}$=CE,再根据F是CE的中点,即可得到F($\sqrt{3}$,2+2$\sqrt{3}$),最后根据反比例函数y=$\frac{k}{x}$的图象过CE的中点F,即可得到k的值.
解答 解:∵正方形ABCD的两个顶点A,D分别在x轴和y轴上,CE⊥y轴于点E,
∴∠CED=∠DOA=90°,∠DCE=∠ADO,CD=DA,
∴△CDE≌△DAO,
∴DE=AO=2,
又∵∠ODA=30°,
∴Rt△AOD中,AD=2AO=4,DO=2$\sqrt{3}$=CE,
∴EO=2+2$\sqrt{3}$,
又∵F是CE的中点,
∴EF=$\sqrt{3}$,
∴F($\sqrt{3}$,2+2$\sqrt{3}$),
∵反比例函数y=$\frac{k}{x}$的图象过CE的中点F,
∴k=$\sqrt{3}$(2+2$\sqrt{3}$)=2$\sqrt{3}$+6,
故答案为:2$\sqrt{3}$+6.
点评 本题主要考查了反比例函数图象上点的坐标特征,正方形的性质以及全等三角形的性质的运用,解题时注意:反比例函数图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
8.下列说法中,正确的是( )
| A. | 同位角相等 | B. | 矩形的对角线一定互相垂直 | ||
| C. | 对角线相等的四边形是矩形 | D. | 四条边相等的四边形是菱形 |
 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF. 如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°…则AD2=$\frac{\sqrt{3}}{2}$,依此类推这样做的第n个菱形ABnCnDn的边ADn的长是($\frac{\sqrt{3}}{2}$)n-1.
如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°…则AD2=$\frac{\sqrt{3}}{2}$,依此类推这样做的第n个菱形ABnCnDn的边ADn的长是($\frac{\sqrt{3}}{2}$)n-1. 如图,AC是?ABCD的对角线,∠BAC=∠DAC,若AB=2,AC=2$\sqrt{3}$,则S?ABCD=2$\sqrt{3}$.
如图,AC是?ABCD的对角线,∠BAC=∠DAC,若AB=2,AC=2$\sqrt{3}$,则S?ABCD=2$\sqrt{3}$.