题目内容
12.如图,在矩形ABCD中,已知A(-3,2),C(2,0),求直线BD的解析式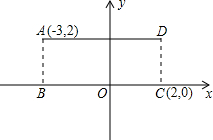
分析 根据矩形的性质和点A、C的坐标求得点B、D的坐标,然后利用待定系数法求直线BD的解析式.
解答  解:∵在矩形ABCD中,A(-3,2),C(2,0),
解:∵在矩形ABCD中,A(-3,2),C(2,0),
∴B(-3,0),D(2,2),
设直线BD的解析式为:y=kx+b(k≠0),
则$\left\{\begin{array}{l}{-3k+b=0}\\{2k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{2}{5}}\\{b=\frac{6}{5}}\end{array}\right.$
所以,直线BD的解析式为:y=$\frac{2}{5}$x+$\frac{6}{5}$.
点评 本题考查了待定系数法求一次函数解析式,矩形的性质,根据矩形的性质求得点B、D的坐标是解题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.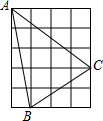 如图,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC,其边长是无理数的有( )
如图,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC,其边长是无理数的有( )
 如图,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC,其边长是无理数的有( )
如图,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC,其边长是无理数的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 将一副三角尺按如图所示方式摆放,若斜边DF∥AB,则∠1的度数为75°.
将一副三角尺按如图所示方式摆放,若斜边DF∥AB,则∠1的度数为75°.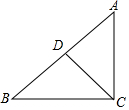 如图,在△ABC中,∠ACB=90°,∠B=35°,CD是AB上的中线,则∠ADC=70°.
如图,在△ABC中,∠ACB=90°,∠B=35°,CD是AB上的中线,则∠ADC=70°.
 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知∠BAC=30°,EF⊥AB于点F,连接DF.