题目内容
2．
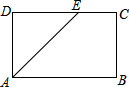如图，在矩形ABCD中，AB=5，BC=3，∠BAD的角平分线与DC交于点E，则CE的长为（ ）| A． | 2 | B． | 2.5 | C． | 3 | D． | 4 |
分析 首先证明△ADE是等腰直角三角形，进而得到CE=DC-DE=AB-AD，计算出答案即可．
解答 解：∵四边形ABCD是矩形，
∴∠BAD=∠D=90°，
∵AE是∠BAD的平分线，
∴△ADE是等腰直角三角形，
∴AD=DE，
∵AB=5，BC=3，
∴CE=DC-DE=AB-AD=2，
故选A．
点评 本题考查了矩形的性质，等腰直角三角形的判定与性质，熟记性质并准确识图是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．下列计算中，正确的是（ ）
| A． | $\sqrt{2}×3\sqrt{2}=4\sqrt{2}$ | B． | $\sqrt{24}$$÷\sqrt{6}$=2 | C． | $\sqrt{12}$$+\sqrt{18}$=6$\sqrt{3}$ | D． | $\sqrt{20}$-$\sqrt{5}$=4 |
10．若关于x的不等式mx-n＞0的解集是x＜$\frac{1}{3}$，则关于x的不等式（m+n）x＞n-m的解集是（ ）
| A． | x＜-$\frac{1}{2}$ | B． | x＞-$\frac{1}{2}$ | C． | x＜$\frac{1}{2}$ | D． | x＞$\frac{1}{2}$ |
17．下列运算正确的是（ ）
| A． | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B． | 2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$ | C． | 2+$\sqrt{2}$=2$\sqrt{2}$ | D． | $\sqrt{3}$-$\sqrt{2}$=1 |
7．
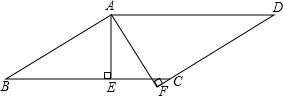如图，在?ABCD中，AE⊥BC于点E，AF⊥DC交DC的延长线于点F，且∠EAF=35°，则∠D等于（ ）
如图，在?ABCD中，AE⊥BC于点E，AF⊥DC交DC的延长线于点F，且∠EAF=35°，则∠D等于（ ）| A． | 65° | B． | 55° | C． | 35° | D． | 25° |
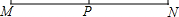如图，已知线段MN═6cm，点P是MN的中点．分别以M、N为圆心，r1cm，r2cm为半径画圆．若点P在⊙M内，又在⊙N外．则r1的范围是r1＞3，r2的范围是0＜r2＜3．