题目内容
2.已知在Rt△ABC中,∠ABC=90°,BD⊥AC于D,若AD:CD=4:1,求sinA,tanA.分析 根据已知条件设AD=4k,CD=k,由射影定理得到BD=2k,由勾股定理得到AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{5}$k,然后由锐角三角函数的定义即可得到结论.
解答  解:如图,∵AD:CD=4:1,
解:如图,∵AD:CD=4:1,
∴设AD=4k,CD=k,
∵∠ABC=90°,BD⊥AC,
由射影定理得:BD2=AD•CD=4k2,
∴BD=2k,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{5}$k,
∴sinA=$\frac{BD}{AB}=\frac{2k}{2\sqrt{5}k}=\frac{\sqrt{5}}{5}$,
tanA=$\frac{BD}{AD}=\frac{2k}{4k}=\frac{1}{2}$.
点评 本题考查了解直角三角形,勾股定理,射影定理,熟练掌握锐角三角函数的定义是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
14.甲、乙两人比赛投篮球,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,表为两人投篮球的记录:
得知他们的成绩一样好,下面有四个a、b的关系式:
①a-b=5;②a+b=18;③a:b=2:1;④a:18=2:3.
其中正确的是( )
| 学生 | 投进球数 | 没投进球数 | 投球次数 |
| 甲 | 10 | 5 | 15 |
| 乙 | a | b | 18 |
①a-b=5;②a+b=18;③a:b=2:1;④a:18=2:3.
其中正确的是( )
| A. | ①②③ | B. | ①③④ | C. | ①②③④ | D. | ②③④ |
12.下列算结果正确的是( )
| A. | -8-(-3)=5 | B. | (-2.5)-(+7.2)=4.7 | C. | (-$\frac{2}{5}$)-(-$\frac{1}{4}$)=-$\frac{3}{20}$ | D. | 5-(-6)=-1 |
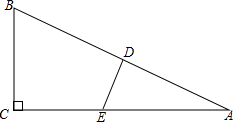 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,∠A=30°,且CE=2cm,求AC的长.
如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,∠A=30°,且CE=2cm,求AC的长.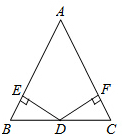 如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.
如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.