题目内容
7．
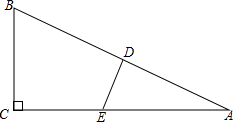如图，在△ABC中，∠C=90°，DE是AB的垂直平分线，∠A=30°，且CE=2cm，求AC的长．
分析 连接BE，根据线段的垂直平分线的性质得到EB=EA，得到∠CBE=∠EBA，根据角平分线的性质得到DE=CE=2cm，根据直角三角形的性质求出AE，得到答案．
解答 解：
连接BE，
∵DE是AB的垂直平分线，
∴EB=EA，
∴∠EBA=∠A=30°，
∴∠CBE=30°，
∴∠CBE=∠EBA，∠C=90°，ED⊥AB，
∴DE=CE=2cm，
∵∠A=30°，
∴AE=2DE=4cm，
∴AC=CE+AE=6cm．
点评 本题考查的是线段的垂直平分线的性质和直角三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键，注意在直角三角形中，30°角所对的直角边等于斜边的一半．
练习册系列答案
相关题目
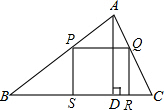一块铁皮呈锐角三角形，它的一边BC=80cm，高AD=60cm．要把它加工成矩形零件PQRS，使矩形的一边SR位于边BC上，另两个顶点P、Q分别在边AB、AC上，请你设计一个加工方案，使矩形零件的面积最大，并求出最大面积．