题目内容
11.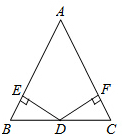 如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.
如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.
分析 先根据HL定理判断出△BDE≌△CDF,由全等三角形的性质可得出∠B=∠C,由此可得出结论.
解答 解:△ABC是等腰三角形.
∵点D是边BC的中点,
∴BD=CD.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在Rt△BDE与Rt△CDF中,
$\left\{\begin{array}{l}BD=CD\\ DE=DF\end{array}\right.$,
∴△BDE≌△CDF,
∴∠B=∠C,
∴△ABC是等腰三角形.
点评 本题考查的是全等三角形的判定与性质,熟知全等三角形的对应边相等是解答此题的关键.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.下列说法不正确的是( )
| A. | 某事件发生的概率为1,则它一定必然会发生 | |
| B. | 某事件发生的概率为O,则它必然不会发生 | |
| C. | 抛一个普通纸杯,杯口不可能向上 | |
| D. | 从一批产品中任取一个为次品是可能的 |
3.一艘船在相距120千米的两个码头间航行,去时顺水用了4小时,回来时逆水用了5小时,则水速为( )
| A. | 2千米/小时 | B. | 3千米/小时 | C. | 4千米/小时 | D. | 5千米/小时 |
1.用配方法解一元二次方程x2-4x-5=0,此方程可变形为( )
| A. | (x-2)2=9 | B. | (x+2)2=9 | C. | (x+2)2=1 | D. | (x-2)2=1 |
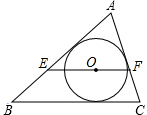 如图,点O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交于点E、F,则线段EF、BE、CF三者间的数量关系是EF=BE+CF.
如图,点O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交于点E、F,则线段EF、BE、CF三者间的数量关系是EF=BE+CF.