题目内容
设G是等腰△ABC底边上的高、AD与腰AC上的中线BE的交点．若AD=18，BE=15，则这个等腰三角形的面积为多少？
考点：等腰三角形的性质,勾股定理
专题：计算题
分析：根据等腰三角形三线合一的性质可得到AD是底边BC的中线，从而得到点G为△ABC的重心，从而不难求得DG，BG的长，再根据勾股定理求得BD的长，最后根据三角形面积公式求解即可．
解答：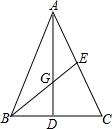
解：∵△ABC是等腰三角形，AD是底边BC的高，
∴AD是底边BC的中线，
∵BE是AC边上的中线，且其与AD交于点G，
∴G为△ABC的重心，
∵AD=18，BE=15，
∴DG=
AD=6，BG=
BE=10，
∴BD=
=8，
∴S△ABC=
BC×AD=144．
解：∵△ABC是等腰三角形，AD是底边BC的高，∴AD是底边BC的中线，
∵BE是AC边上的中线，且其与AD交于点G，
∴G为△ABC的重心，
∵AD=18，BE=15，
∴DG=
| 1 |
| 3 |
| 2 |
| 3 |
∴BD=
| BG2-DG2 |
∴S△ABC=
| 1 |
| 2 |
点评：此题主要考查等腰三角形的性质及勾股定理的综合运用．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
如图，平行四边形ABCD中，∠A是它的外角的若a＞1，b是有理数，且ab+a-b=2
，则ab-a-b等于（ ）
| 2 |
A、
| ||
| B、2或-2 | ||
| C、-2 | ||
| D、2 |
适合方程
+3x2+6xz+2y+y2+3z2+1=0 \；的x、y、z的值适合（ ）
| x2-2xy+y2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|