题目内容
1.已知:AB、CD为⊙O的直径,弦BE交CD于点F,连接DE交AB于点G,GO=GD.(1)如图1,求证:DE=DF;
(2)如图2,作弦AK∥DC,AK交BE于点N,连接CK,求证:四边形KNFC为平行四边形;
(3)如图3,作弦CH,连接DH,∠CDH=3∠EDH,CH=2$\sqrt{11}$,BE=4$\sqrt{7}$,求DH的长.

分析 (1)如图1中,连接BC.欲证明DE=DF,只要证明∠E=∠EFD.
(2)如图2中,连接AD、DK、BC.首先证明∠ADC=∠KCD,再证明∠EFD=∠ADC,即可推出∠EFD=∠KCD,推出KC∥FN,由此即可解决问题.
(3)如图3中,作ON⊥BE于N,HK⊥CD于K,连接EO.想办法证明△OHK≌△OBN,推出HK=BN=2$\sqrt{7}$,再证明△CKH∽△CHD,得$\frac{CK}{CH}$=$\frac{HK}{DH}$,利用勾股定理求出KC即可解决问题.
解答 (1)证明:如图1中,连接BC.
∵OB=OC,
∴∠C=∠OBC=∠E,
∵GO=GD,
∴∠D=∠GOD=∠EBC=∠BOC,
∵∠OBC=∠EBC+∠EBA,∠EFD=∠BOC+∠EBA,
∵∠EBC=∠BOC,
∴∠OBC=∠EFD=∠E,
∴DE=DF.
(2)证明:如图2中,连接AD、DK、BC.
∵AK∥CD,
∴∠AKD=∠KDC,
∴$\widehat{AD}$=$\widehat{KC}$,
∴$\widehat{DK}$=$\widehat{AC}$,
∴∠ADC=∠KCD,
∵∠ADO=∠OBC=∠OCB=∠E=∠EFD,
∴∠KCD=∠EFD,
∴KC∥FN,∵KN∥FC,
∴四边形KNFC是平行四边形.
(3)解:如图3中,作ON⊥BE于N,HK⊥CD于K,连接EO.
∵ON⊥EB,
∴EN=BN=2$\sqrt{7}$,
∵∠CDH=3∠EDH,
设∠EDH=x,则∠CDH=3x,∠OHD=∠ODH=3x,∠HOC=∠D+∠OHD=6x,∠GOD=∠GDO=∠BOC=4x,∠HOB=∠HOC+∠BOC=10x,∠EOC=∠ODE+∠OED=8x,∠EOB=∠EOC+∠BOC=12x,
∵∠BON=∠EON=6x,
∴∠HOK=∠BON=6x,
在△OHK和△OBN中,
$\left\{\begin{array}{l}{∠HOK=∠BON}\\{∠KHO=∠ONB}\\{OH=OB}\end{array}\right.$,
∴△OHK≌△OBN,
∴HK=BN=2$\sqrt{7}$,
在Rt△CHK中,CK=$\sqrt{H{C}^{2}-H{K}^{2}}$=$\sqrt{(2\sqrt{11})^{2}-(2\sqrt{7})^{2}}$=4,
∵CD是直径,
∴∠CHD=∠CKH=90°,
∵∠C=∠C,
∴△CKH∽△CHD,
∴$\frac{CK}{CH}$=$\frac{HK}{DH}$,
∴DH=$\frac{CH•HK}{CK}$=$\frac{2\sqrt{11}×2\sqrt{7}}{4}$=$\sqrt{77}$.
点评 本题考查圆综合题、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理、平行线的性质等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线,构造全等三角形解决问题,本题的突破点是证明△OHK≌△OBN,属于中考压轴题.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案| A. | 单项式-34a2b5的次数是11次 | |
| B. | 已知a是有理数,且|a|=-a,则有理数a在数轴上的对应点在原点的左边 | |
| C. | 无理数的绝对值一定是非负数 | |
| D. | 延长线段BA到C,使AC=2BC |
| A. | y=x2+2 | B. | y=x2-2 | C. | y=(x+2)2 | D. | y=(x-2)2 |

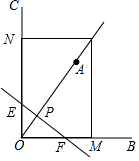 如图,∠BOC=90°,点A在∠BOC的内部,OA=2,∠AOC=30°,点P,Q分别从点O,A同时出发,均以每秒1个单位长度的速度沿OA方向运动.过点P作直线l⊥OA于P,过点Q作QM⊥OB于点M,QN⊥OC于点N,设点P运动时间为t(s)
如图,∠BOC=90°,点A在∠BOC的内部,OA=2,∠AOC=30°,点P,Q分别从点O,A同时出发,均以每秒1个单位长度的速度沿OA方向运动.过点P作直线l⊥OA于P,过点Q作QM⊥OB于点M,QN⊥OC于点N,设点P运动时间为t(s)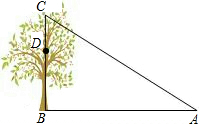 如图在一棵树的10m高的D处有两只猴子,其中一只猴子爬下树走到离树20m处的池塘A处,另一只爬到树顶后直接跃向池塘A处.如果两只猴子所经过的距离相等,试问这棵树高15m.
如图在一棵树的10m高的D处有两只猴子,其中一只猴子爬下树走到离树20m处的池塘A处,另一只爬到树顶后直接跃向池塘A处.如果两只猴子所经过的距离相等,试问这棵树高15m. 如图,菱形ABCD的对角线AC、BD相交于点O,AC=8,BD=6,则此菱形的周长为20.
如图,菱形ABCD的对角线AC、BD相交于点O,AC=8,BD=6,则此菱形的周长为20.