题目内容
18．
如图，菱形ABCD的对角线AC、BD相交于点O，AC=8，BD=6，则此菱形的周长为20．
分析 根据菱形对角线互相垂直平分的性质，可以求得BO=OD，AO=OC，在Rt△AOB中，根据勾股定理可以求得AB的长，即可求菱形ABCD的周长．
解答 解：四边形ABCD是菱形，
∴AB=BC=CD=AD，BO=OD=3，AO=OC=4，AC⊥BD，
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=5，
故菱形的周长为4×5=20．
故答案为：20．
点评 本题考查了勾股定理在直角三角形中的运用，考查了菱形各边长相等的性质，本题中根据勾股定理计算AB的长是解题的关键．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
9．下列各数中，比-1小的数是（ ）
| A． | -2 | B． | -$\frac{1}{2}$ | C． | 0 | D． | -（-2） |
6．
盘秤是一种常见的称量工具，指针转过的角度与被称物体的重量有一定的关系，如下表所示：
（1）请直接写出a、b的值；
（2）指针转过的角度不得超过360°，否则盘秤会受损，称量22千克的物品会对盘秤造成损伤吗？说说你的理由．
（3）某顾客在一家水果店购买水果，用这种盘秤称量两次，第二次的数量是第一次数量的2倍少3千克，且指针第二次转过的角度比第一次大108°，该顾客一共购买了多少千克水果？
盘秤是一种常见的称量工具，指针转过的角度与被称物体的重量有一定的关系，如下表所示：| 重量（单位：千克） | 0 | 1 | 2 | 2.5 | 3 | … | b |
| 指针转过的角度 | 0° | 18° | 36° | a° | 54° | … | 180° |
（2）指针转过的角度不得超过360°，否则盘秤会受损，称量22千克的物品会对盘秤造成损伤吗？说说你的理由．
（3）某顾客在一家水果店购买水果，用这种盘秤称量两次，第二次的数量是第一次数量的2倍少3千克，且指针第二次转过的角度比第一次大108°，该顾客一共购买了多少千克水果？
13．若关于x的一元二次方程a（x-x1）（x-x2）=0（a≠0且x1≠x2）与关于x的一元一次方程dx+e=0（d≠0）有一个公共解x=x1，且方程a（x-x1）（x-x2）+dx+e=0只有一个解，则（ ）
| A． | a（x1-x2）=d | B． | a（x2-x1）=d | C． | a（x1-x2）2=d | D． | a（x1+x2）2=d |
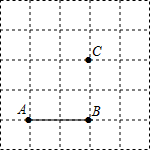如图，己知线段AB及点C，在方格纸上画图并回答问题．