题目内容
13.将抛物线y=x2向上平移2个单位后,所得的抛物线的函数表达式为( )| A. | y=x2+2 | B. | y=x2-2 | C. | y=(x+2)2 | D. | y=(x-2)2 |
分析 求出平移后的抛物线的顶点坐标,然后利用顶点式形式写出即可.
解答 解:∵抛物线y=x2向上平移2个单位后的顶点坐标为(0,2),
∴所得抛物线的解析式为y=x2+2.
故选:A.
点评 本题考查了二次函数图象与几何变换,此类题目利用顶点的平移确定抛物线函数图象的变化更简便.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字;州、爱、我、福、游、美.现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是( )
| A. | 我爱美 | B. | 福州游 | C. | 爱我福州 | D. | 美我福州 |
4.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
| A. | 两点确定一条直线 | B. | 垂线段最短 | ||
| C. | 两点之间线段最短 | D. | 三角形两边之和大于第三边 |
8.某机加工车间共有26名工人,现要加工2100个A零件,1200个B零件,已知每人每天加工A零件30个或B零件20个,问怎样分工才能确保同时完成两种零件的加工任务(每人只能加工一种零件)?设安排x人加工A零件,由题意列方程得( )
| A. | $\frac{2100}{x}$×30=$\frac{1200}{36-x}$×20 | B. | $\frac{2100}{x}$=$\frac{1200}{36-x}$ | ||
| C. | $\frac{2100}{20x}$=$\frac{1200}{30(26-x)}$ | D. | $\frac{2100}{30x}=\frac{1200}{20(26-x)}$ |
9.下列各数中,比-1小的数是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 0 | D. | -(-2) |

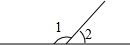 如图,∠1>∠2,那么∠2与$\frac{1}{2}$(∠1-∠2)的关系是互余.
如图,∠1>∠2,那么∠2与$\frac{1}{2}$(∠1-∠2)的关系是互余.