题目内容
15. 如图,△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到点E,使∠BDE=∠E,连接ED并延长交AC于点F,已知∠DAC=58°.
如图,△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到点E,使∠BDE=∠E,连接ED并延长交AC于点F,已知∠DAC=58°.(1)求∠ABC的度数;
(2)求∠AFD的度数.
分析 (1)由垂直的定义得到∠ADC=90°,根据三角形的内角和得到∠C=32°,于是得到结论;
(2)由已知条件和三角形的外角的性质得到∠ABC=2∠E,求得∠E=∠C,由于∠BDE=∠CDF,于是得到∠FDC=∠C=32°,即可得到结果.
解答 解:(1)∵AD⊥BC,
∴∠ADC=90°,
∵∠DAC=58°,
∴∠C=32°,
∴∠ABC=2∠C=64°;
(2)∵∠BDE=∠E,∠ABC=∠∠E+∠BDE,
∴∠ABC=2∠E,
∴∠E=∠C,
∵∠BDE=∠CDF,
∴∠FDC=∠C=32°,
∴∠AFD=2∠C=64°.
点评 本题考查了三角形的内角和,三角形的外角的性质,直角三角形的性质,熟练掌握三角形的内角和是解题的关键.

练习册系列答案
相关题目
12.将104.6402精确到0.01为( )
| A. | 104 | B. | 104.6 | C. | 104.64 | D. | 104.640 |
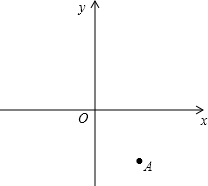 已知函数y=mx与y=kx+b的图象经过点A(3,-4),且y=kx+b的图象交y轴于点B,若△OAB是以OA为腰的等腰三角形,其中O为坐标原点
已知函数y=mx与y=kx+b的图象经过点A(3,-4),且y=kx+b的图象交y轴于点B,若△OAB是以OA为腰的等腰三角形,其中O为坐标原点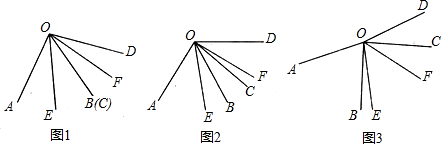
 图1中共有6个三角形,图2中有50个正方形.
图1中共有6个三角形,图2中有50个正方形.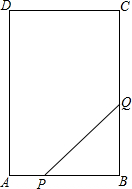 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB边向点B以1cm/s的速度运动,同时,点Q从点B出发沿BC边向点C以2cm/s的速度运动,P,Q两点在分别到达B,C两点后就停止运动,设经过ts时,△PBQ的面积为S cm2
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB边向点B以1cm/s的速度运动,同时,点Q从点B出发沿BC边向点C以2cm/s的速度运动,P,Q两点在分别到达B,C两点后就停止运动,设经过ts时,△PBQ的面积为S cm2