题目内容
11.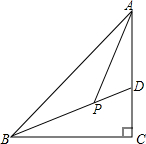 如图,在△ABC中,∠C=90°,BD平分∠ABC且交AC于D,点P在BD上,且∠APB=135°,AP是∠BAC的平分线吗?说明理由.
如图,在△ABC中,∠C=90°,BD平分∠ABC且交AC于D,点P在BD上,且∠APB=135°,AP是∠BAC的平分线吗?说明理由.
分析 根据三角形外角的性质得出∠ADP=∠2+∠C,∠APB=∠4+∠ADP,得到∠APB=∠2+∠4+∠C,从而得出∠2+∠4=45°,根据三角形外角的性质求得∠1+∠3=∠APD=45°,所以∠2+∠4=∠1+∠3,进而即可证得结论.
解答 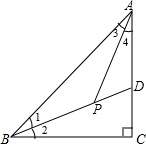 解:AP是∠BAC的平分线,
解:AP是∠BAC的平分线,
理由:∵∠ADP=∠2+∠C,∠APB=∠4+∠ADP,
∴∠APB=∠2+∠4+∠C,
∵∠C=90°,∠APB=135°,
∴∠2+∠4=45°,
∵∠APB=135°,
∴∠APD=45°,
∵∠1+∠3=∠APD,
∴∠1+∠3=45°,
∵∠1=∠2,
∴∠3=∠4,
∴AP是∠BAC的平分线.
点评 本题考查了三角形角平分线的性质和三角形外角的性质,熟练掌握性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知△A1BC中,∠A1=64°,BA2平分∠A1BC,CA2平分∠A1CE,BA2、CA2相交于A2;BA3平分∠A2BC,CA3平分∠A2CE,BA3、CA3相交于A3,依此类推.
如图,已知△A1BC中,∠A1=64°,BA2平分∠A1BC,CA2平分∠A1CE,BA2、CA2相交于A2;BA3平分∠A2BC,CA3平分∠A2CE,BA3、CA3相交于A3,依此类推. 已知函数y=mx与y=kx+b的图象经过点A(3,-4),且y=kx+b的图象交y轴于点B,若△OAB是以OA为腰的等腰三角形,其中O为坐标原点
已知函数y=mx与y=kx+b的图象经过点A(3,-4),且y=kx+b的图象交y轴于点B,若△OAB是以OA为腰的等腰三角形,其中O为坐标原点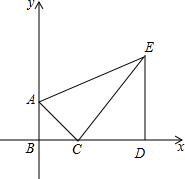 已知,如图,B为坐标原点,A(0,3),D(10,0),E(10,8),点C是线段BD上的动点.
已知,如图,B为坐标原点,A(0,3),D(10,0),E(10,8),点C是线段BD上的动点.