题目内容
17.一个不透明的口袋中装有3个黑球和5个白球,这些球的大小、质地完全相同,从口袋中随机摸出1个球,这个球是黑球的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
分析 根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.本题球的总数为8,黑球的数目为3.
解答 解:根据题意可得:一袋中装有8个球,其中3个黑球5个白球,
任意摸出1个,摸到黑球的概率是=$\frac{3}{8}$,
故选:B.
点评 本题考查的是概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
2.下列因式分解正确的是( )
| A. | x2-xy+x=x(x-y) | B. | x2-2x+4=(x-1)2+3 | ||
| C. | ax3-9=a(x+3)(x-3) | D. | a3-2a2b+ab2=a(a-b)2 |
 用6m长的铝合金型材做一个形状如图所示的矩形窗框,若窗框的面积为1.5m2(铝合金型材宽度不计),求该窗框的长和宽各为多少?
用6m长的铝合金型材做一个形状如图所示的矩形窗框,若窗框的面积为1.5m2(铝合金型材宽度不计),求该窗框的长和宽各为多少? 如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC, 如图所示,在直角坐标系中放置一个矩形ABCD,其中AB=2,AD=1,将矩形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为$\frac{9}{4}$π+2.
如图所示,在直角坐标系中放置一个矩形ABCD,其中AB=2,AD=1,将矩形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为$\frac{9}{4}$π+2.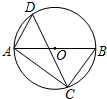 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=54°,则∠BAC=36°.
如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=54°,则∠BAC=36°. 如图,已知AC,BC分别平分∠QAB,∠ABN,且∠1与∠2互余,求证:PQ∥MN.
如图,已知AC,BC分别平分∠QAB,∠ABN,且∠1与∠2互余,求证:PQ∥MN.