题目内容
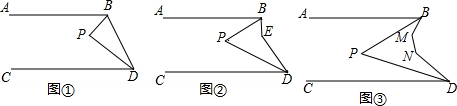
13.如图1.己知AB∥CD,BP、DP分别平分∠ABD、∠BDC.(1)∠BPD=90°;
(2)如图②,将BD改为折线BED,BP、DP分别平分∠ABE、∠EDC,其余条件不变,若∠BED=120°,求∠BPD的度数:并进一步猜想∠BPD与∠BED之间的数量关系;
(3)如图3,若∠BMN=132°,∠MND=144°,BP、DP分别平分∠ABM、∠CDN,那么∠BPD=48°.
分析 (1)先根据平行线的性质得出∠ABD+∠BDC=∠180°,再根据角平分线的定义得出∠PBD+∠PDB的度数,由三角形内角和定理即可得出结论;
(2)连接BD,先求出∠EBD+∠EDB的度数,再由平行线的性质得出∠ABD+∠CDB的度数,由角平分线的性质得出∠PBE+∠PDE的度数,根据∠BPD=180°-∠PBE-PDE-∠EBD-∠EDB即可得出结论.
(3)连接BD,先求出∠MBD+∠NDB的度数,再求出∠PBM+∠PDN的度数,再利用三角形内角和定理即可解决.
解答 解:(1)∵AB∥CD,
∴∠ABD+∠BDC=∠180°,
∵BP、DP分别平分∠ABD、∠BDC,
∴∠PBD+∠PDB=90°,
∴∠BPD=180°-90°=90°.
故答案为:90;
(2) 连接BD,
连接BD,
∵∠BED=120°,
∴∠EBD+∠EDB=60°,
∵AB∥CD,
∴∠ABD+∠CDB=180°,
∵BP、DP分别平分∠ABE、∠EDC,
∴∠PBE=$\frac{1}{2}$∠ABE,∠PDE=$\frac{1}{2}$∠CDE,
∴∠PBE+∠PDE=$\frac{1}{2}$(180°-60°)=60°,
∴∠BPD=180°-∠PBE-PDE-∠EBD-∠EDB=60°.
猜想:∠BPD=$\frac{1}{2}$∠BED.
(3)连接BD,
∵∠BMN=132°,∠MND=144°,
∴∠MBD+∠NDB=360°-(132°+144°)=84°,
∵BP、DP分别平分∠ABM、∠NDC,
∴∠PBM=$\frac{1}{2}$∠ABM,∠PDN=$\frac{1}{2}$∠CDN,
∴∠PBM+∠PDN=$\frac{1}{2}$(180°-84°)=48°,
∴∠BPD=180°-(∠MBD+∠NDB)-(∠PBM+∠PDN)=48°.
故答案为48°.
点评 本题考查的是平行线的性质,角平分线的性质,三角形、四边形内角和定理,解题的关键是这些知识的灵活应用,学会添加辅助线,把问题转化为三角形或四边形,属于中考常考题型.

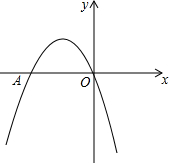 如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).
如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).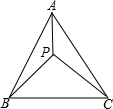 已知:如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.
已知:如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.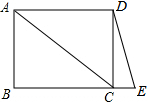 四边形ABCD是矩形,点E是射线BC上一点,连接AC,DE.如图,BE=AC,若∠ACB=40°,求∠E的度数.
四边形ABCD是矩形,点E是射线BC上一点,连接AC,DE.如图,BE=AC,若∠ACB=40°,求∠E的度数.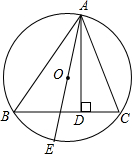 如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证:
如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证: