题目内容
3.设a1,a2,…,a2014,a2015是从1,0,-1这三个数中取值的一列数,若a1+a2+…+a2014+a2015=69,(a1+1)2+(a2+1)2+…+(a2014+1)2+(a2015+1)2=4002,则a1,a2,…,a2015中为0的个数是166.分析 设a1,a2,…,a2014,a2015中有x个-1,y个0,则有x+69个1,由此可得出x+y+x+69=2015,数列a1+1,a2+1,…,a2014+1,a2015+1中有x个0,y个1,x+69个2,由此得出y+4(x+69)=4002,二者联立成方程组,解方程组即可得出结论.
解答 解:设a1,a2,…,a2014,a2015中有x个-1,y个0,则有x+69个1,则a1+1,a2+1,…,a2014+1,a2015+1中有x个0,y个1,x+69个2,
根据题意得:$\left\{\begin{array}{l}{x+y+x+69=2015}\\{y+4(x+69)=4002}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=890}\\{y=166}\end{array}\right.$.
故答案为:166.
点评 本题考查了数字的变化依据二元一次方程组的应用,解题的关键是找出关于x、y的二元一次方程组.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程(方程组)是关键.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | (3,2)和(2,3)表示一个点 | B. | 点($\sqrt{3}$,0)在x轴的正半轴上 | ||
| C. | 点(-2,4)在第四象限 | D. | 点(3,-1)到x轴的距离为3 |
15.±$\sqrt{(-16)^{2}}$的值是( )
| A. | ±16 | B. | ±4 | C. | 16 | D. | -16 |
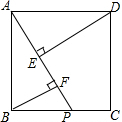 如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象.
如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象.