题目内容
8.方程(x2-x+1)2-x2+x-3=0的实根为x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.分析 令t=x2-x+1,将原方程转化为关于t的一元二次方程求出t的值,就t的不同值分别列出对应的关于x的方程求解即可.
解答 解:令t=x2-x+1,则原方程可化为:t2-(t+2)=0,即t2-t-2=0,
左边因式分解得:(t+1)(t-2)=0,
∴t1=-1,t2=2,
当t=-1时,x2-x+1=-1,即x2-x+2=0,
∵△=(-1)2-4×1×2=-7,
∴方程无解;
当t=2时,x2-x+1=2,即x2-x-1=0,
解得:x=$\frac{1±\sqrt{5}}{2}$;
则方程的根为:x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$,
故答案为:x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.
点评 本题考查了用换元法解方程,解题关键是能准确的找出可用替换的代数式x2-x+1,再用字母t代替解方程.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
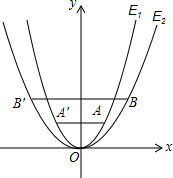 如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.

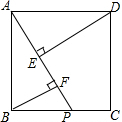 如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象.
如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象.