题目内容
5.若(a2+b2)(a2+b2-8)+16=0,那么a2+b2的值为4.分析 令a2+b2=t,将原方程化为关于t的一元二次方程,解得t的值即可知a2+b2的值,
解答 解:令a2+b2=t,则原方程可变形成:t(t-8)+16=0,
即t2-8t+16=0,
∴(t-4)2=0,
可得:t1=t2=4,即a2+b2=4,
故答案为:4.
点评 本题主要考查换元法解一元二次方程,换元法即是整体思想的考查,解题的关键是找到这个整体.

练习册系列答案
相关题目
15.下列二次根式有意义的范围为x≥2的是( )
| A. | $\sqrt{\frac{1}{x-2}}$ | B. | $\sqrt{x-2}$ | C. | $\sqrt{\frac{1}{x+2}}$ | D. | $\sqrt{x+2}$ |
14.下列说法正确的是( )
| A. | (3,2)和(2,3)表示一个点 | B. | 点($\sqrt{3}$,0)在x轴的正半轴上 | ||
| C. | 点(-2,4)在第四象限 | D. | 点(3,-1)到x轴的距离为3 |
15.±$\sqrt{(-16)^{2}}$的值是( )
| A. | ±16 | B. | ±4 | C. | 16 | D. | -16 |
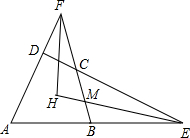 如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.