题目内容
11.因式分解:abc+a+b+c-ab-ac-bc-1=(a-1)(b-1)(c-1).分析 首先重新分组,进而利用提取公因式法分解因式得出即可.
解答 解:abc+a+b+c-ab-ac-bc-1
=ab(c-1)+a(1-c)+b(1-c)+(c-1)
=ab(c-1)-a(c-1)-b(c-1)+(c-1)
=(c-1)(ab-a-b+1)
=(c-1)[a(b-1)-(b-1)]
=(c-1)(b-1)(a-1).
故答案为:(a-1)(b-1)(c-1).
点评 此题主要考查了分组分解法因式分解,正确分组得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.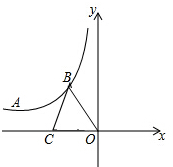 如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )
如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )
 如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )
如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
6. 寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
 寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )| A. | 小明调查了100名同学 | |
| B. | 所得数据的众数是40小时 | |
| C. | 所得数据的中位数是30小时 | |
| D. | 全区有七年级学生6000名,寒假阅读总时间在20小时(含20小时)以上的约有5000名 |
3.反比例函数y=$\frac{1-k}{x}$图象的每条曲线上y都随x增大而增大,则k的取值范围是( )
| A. | k>1 | B. | k>0 | C. | k<1 | D. | k<0 |
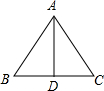 如图,等边△ABC中,AD为高,若AB=6,则CD的长度为3.
如图,等边△ABC中,AD为高,若AB=6,则CD的长度为3.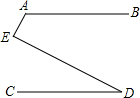 如图所示,若AB∥CD,则∠A,∠D,∠E的度数之间的等量关系是∠A+∠E-∠D=180°.
如图所示,若AB∥CD,则∠A,∠D,∠E的度数之间的等量关系是∠A+∠E-∠D=180°.