题目内容
20.在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C; ④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据直角三角形的判定对各个条件进行分析,从而得到答案.
解答 解:①、∵∠A+∠B=∠C=90°,∴△ABC是直角三角形,故小题正确;
②、∵∠A:∠B:∠C=1:2:3,∴∠A=30°,∠B=60°,∠C=90°,△ABC是直角三角形,故本小题正确;
③、设∠A=x,∠B=2x,∠C=3x,则x+2x+3x=180°,解得x=30°,故3x=90°,△ABC是直角三角形,故本小题正确;
④∵设∠C=x,则∠A=∠B=2x,∴2x+2x+x=180°,解得x=36°,∴2x=72°,故本小题错误;
⑤∠A=2∠B=3∠C,
∴∠A+∠B+∠C=∠A+$\frac{1}{2}$∠A+$\frac{1}{3}∠$A=180°,
∴∠A=$\frac{1080}{11}$°,故本小题错误.
综上所述,是直角三角形的是①②③共3个.
故选B.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
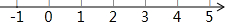 解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x>1}&{①}\\{1-x≥-3}&{②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x>1}&{①}\\{1-x≥-3}&{②}\end{array}\right.$