题目内容
2.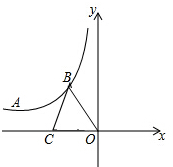 如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )
如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
分析 根据A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),可以求得k的值,根据B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,可知OB=BC,设出点B的坐标,即可表示出△BCO面积,本题得以解决.
解答 解:∵A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),
∴k=(-4)×2=-8,
∴$y=\frac{-8}{x}$,
又∵B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,
∴设点B的坐标为(a,$\frac{-8}{a}$),OB=CB,
∴OC=-2a,点B到OC的距离为$\frac{-8}{a}$,
∴${S}_{△BOC}=\frac{(-2a)×(\frac{-8}{a})}{2}$=8,
故选C.
点评 本题考查反比例函数系数k的几何意义、反比例函数图象上点的坐标特征,解题的关键是明确反比例函数图象的特点,利用数形结合的思想解答问题.

练习册系列答案
相关题目
14.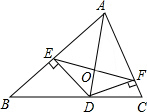 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是( )
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是( )
 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是( )
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是( )| A. | DE=DF | B. | AE=AF | C. | OD=OF | D. | OE=OF |
 一名儿童行走在如图所示的地板上,当他随意停下时,最终停在阴影部分的概率是$\frac{1}{3}$.
一名儿童行走在如图所示的地板上,当他随意停下时,最终停在阴影部分的概率是$\frac{1}{3}$. 如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和
如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和