题目内容
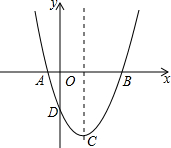 如图,抛物线y=(x-1)2-4的图象与x轴交于的A、B两点,与y轴交于点D,抛物线的顶点为C.
如图,抛物线y=(x-1)2-4的图象与x轴交于的A、B两点,与y轴交于点D,抛物线的顶点为C.(1)求△ABD的面积;
(2)求△ABC的面积;
(3)点P是抛物线上一动点,当△ABP的面积为4时,求所有符合条件的点P的坐标;
(4)点P是抛物线上一动点,当△ABP的面积为8时,求所有符合条件的点P的坐标;
(5)点P是抛物线上一动点,当△ABP的面积为10时,求所有符合条件的点P的坐标.
考点:二次函数综合题
专题:
分析:(1)求得A、B、D点的坐标即可求得△ABD的面积;
(2)求得A、B、C点的坐标即可求得△ABD的面积;
(3)设点P的坐标为(x0,y0),由△ABP的面积为4得到
AB•|y0|=4,从而求得y0=±2,即(x0-1)2-4=±2,求得x的值后即可求得点P的坐标;
(4)设点P的坐标为(x0,y0),由△ABP的面积为8得到
AB•|y0|=8,从而求得y0=±4,即(x0-1)2-4=±4,求得x的值后即可求得点P的坐标;
(5)设点P的坐标为(x0,y0),由△ABP的面积为10得到
AB•|y0|=5,从而求得y0=±5,即(x0-1)2-4=±5,求得x的值后即可求得点P的坐标;
(2)求得A、B、C点的坐标即可求得△ABD的面积;
(3)设点P的坐标为(x0,y0),由△ABP的面积为4得到
| 1 |
| 2 |
(4)设点P的坐标为(x0,y0),由△ABP的面积为8得到
| 1 |
| 2 |
(5)设点P的坐标为(x0,y0),由△ABP的面积为10得到
| 1 |
| 2 |
解答:解:令y=0,
即(x-1)2-4=0,
解得x=3或x=-1,
知A(-1,0),B(3,0),
即AB=4,
令x=0得:y=-3,
知:D(0,-3),
故S△ABD=
AB•OD=
×4×3=6;
(2)由y=(x-1)2-4知顶点C的坐标为(1,-4),
故S△ABC=
×4×4=8;
(3)设点P的坐标为(x0,y0),
又由△ABP的面积为4,
知
AB•|y0|=4,
即
×4×|y0|=4,
即|y0|=2,
即y0=±2,
即(x0-1)2-4=±2
解得x=1+
或x=1-
或x=1+
或x=1-
.
即P(1+
,-2)或P(1-
,-2)或(1+
,-2)或(1-
,-2);
(4)由△ABP的面积为8,
知
AB•|y0|=8,
即
×4×|y0|=8,
即|y0|=4,
即y0=±4,
即(x0-1)2-4=±4
解得x=1+2
或x=1-2
或x=1.
即P(1+2
,-2)或P(1-2
,-2)或(1,-2);
(5)由△ABP的面积为10,
知
AB•|y0|=10,
即
×4×|y0|=10,
即|y0|=5,
即y0=±5,
即(x0-1)2-4=±5
解得x=3或x=-3.
即P(3,-2)或P(-3,-2);
即(x-1)2-4=0,
解得x=3或x=-1,
知A(-1,0),B(3,0),
即AB=4,
令x=0得:y=-3,
知:D(0,-3),
故S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
(2)由y=(x-1)2-4知顶点C的坐标为(1,-4),
故S△ABC=
| 1 |
| 2 |
(3)设点P的坐标为(x0,y0),
又由△ABP的面积为4,
知
| 1 |
| 2 |
即
| 1 |
| 2 |
即|y0|=2,
即y0=±2,
即(x0-1)2-4=±2
解得x=1+
| 2 |
| 2 |
| 6 |
| 6 |
即P(1+
| 2 |
| 2 |
| 6 |
| 6 |
(4)由△ABP的面积为8,
知
| 1 |
| 2 |
即
| 1 |
| 2 |
即|y0|=4,
即y0=±4,
即(x0-1)2-4=±4
解得x=1+2
| 2 |
| 2 |
即P(1+2
| 2 |
| 2 |
(5)由△ABP的面积为10,
知
| 1 |
| 2 |
即
| 1 |
| 2 |
即|y0|=5,
即y0=±5,
即(x0-1)2-4=±5
解得x=3或x=-3.
即P(3,-2)或P(-3,-2);
点评:本题考查了二次函数的综合知识,解题的关键是求得抛物线与坐标轴的交点坐标,后三个题目解题方法几乎一致,只是数据不同,难度中等偏上.

练习册系列答案
相关题目
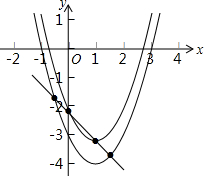 如图,抛物线c1:y=(x-1)2-
如图,抛物线c1:y=(x-1)2- 平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=60°,若CF=2,CE=3,求平行四边形ABCD周长.
平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=60°,若CF=2,CE=3,求平行四边形ABCD周长.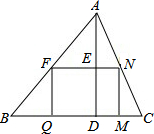 有一块锐角三角形铁片ABC,已知最长边BC=12cm,高AD=8cm,要把它加工成一个矩形铁片,使矩形的一边在BC上,其余的两个顶点分别在AB、AC上,且矩形的长是宽的3倍,求矩形的面积.
有一块锐角三角形铁片ABC,已知最长边BC=12cm,高AD=8cm,要把它加工成一个矩形铁片,使矩形的一边在BC上,其余的两个顶点分别在AB、AC上,且矩形的长是宽的3倍,求矩形的面积.