题目内容
a2+（a+1）2+（a2+a）2，并计算：62+72+422．
考点：因式分解的应用
专题：
分析：把原式整理，利用完全平方公式因式分解即可；利用分解的结果代入数据计算得出结果．
解答：解：a2﹢﹙a﹢1﹚2﹢﹙a2﹢a﹚2
=a2+a2+2a+1+﹙a2﹢a﹚2
=﹙a2﹢a﹚2+2（a2+a）+1
=（a2﹢a+1）2，
则62+72+422=（62+7+1）2=442=1936．
=a2+a2+2a+1+﹙a2﹢a﹚2
=﹙a2﹢a﹚2+2（a2+a）+1
=（a2﹢a+1）2，
则62+72+422=（62+7+1）2=442=1936．
点评：此题考查因式分解的运用，根据算式的特点，灵活选用适当的方法因式分解．
练习册系列答案
轻松暑假总复习系列答案
相关题目
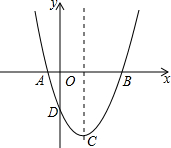如图，抛物线y=（x-1）2-4的图象与x轴交于的A、B两点，与y轴交于点D，抛物线的顶点为C．