题目内容
已知函数y=mx2-6x+19(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
考点:抛物线与x轴的交点,二次函数图象上点的坐标特征
专题:
分析:(1)根据解析式可知,当x=0时,与m值无关,故可知不论m为何值,函数y=mx2-6x+19的图象都经过y轴上一个定点(0,19).
(2)应分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;
②当函数为二次函数时,利用根与系数的关系解答.
(2)应分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;
②当函数为二次函数时,利用根与系数的关系解答.
解答:解:(1)当x=0时,y=19.
所以不论m为何值,函数y=mx2-6x+19的图象都经过y轴上一个定点(0,19);
(2)①当m=0时,函数y=-6x+19的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2-6x+19的图象与x轴只有一个交点,则方程mx2-6x+19=0有两个相等的实数根,
所以△=(-6)2-4×19m=0,m=
.
综上,若函数y=mx2-6x+1的图象与x轴只有一个交点,则m的值为0或
.
所以不论m为何值,函数y=mx2-6x+19的图象都经过y轴上一个定点(0,19);
(2)①当m=0时,函数y=-6x+19的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2-6x+19的图象与x轴只有一个交点,则方程mx2-6x+19=0有两个相等的实数根,
所以△=(-6)2-4×19m=0,m=
| 9 |
| 19 |
综上,若函数y=mx2-6x+1的图象与x轴只有一个交点,则m的值为0或
| 9 |
| 19 |
点评:此题考查了抛物线与x轴的交点或一次函数与x轴的交点,是典型的分类讨论思想的应用.

练习册系列答案
相关题目
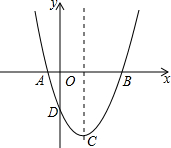 如图,抛物线y=(x-1)2-4的图象与x轴交于的A、B两点,与y轴交于点D,抛物线的顶点为C.
如图,抛物线y=(x-1)2-4的图象与x轴交于的A、B两点,与y轴交于点D,抛物线的顶点为C.