题目内容
6.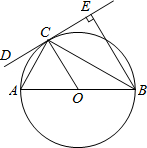 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.(1)求证:BC平分∠ABE;
(2)若∠A=60°OA=4,求CE的长.
分析 (1)根据切线的性质得OC⊥DE,则可判断OC∥BE,根据平行线的性质得∠OCB=∠CBE,加上∠OCB=∠CBO,所以∠OBC=∠CBE,
(2)利用圆周角定理得到∠ACB=90°,再根据正弦的定义可计算出BC=4$\sqrt{3}$,然后在Rt△CBE中可得到CE=$\frac{1}{2}$BC=2$\sqrt{3}$.
解答 (1)证明:∵CD是⊙O的切线,
∴OC⊥DE,
而BE⊥DE,
∴OC∥BE,
∴∠OCB=∠CBE,
而OB=OC,
∴∠OCB=∠CBO,
∴∠OBC=∠CBE,
即BC平分∠ABE;
(2)解:∵AB为直径,
∴∠ACB=90°,
∵sinA=$\frac{BC}{AB}$,
∴BC=8sin60°=4$\sqrt{3}$,
∵∠OBC=∠CBE=30°,
在Rt△CBE中,CE=$\frac{1}{2}$BC=2$\sqrt{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了解直角三角形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.雾霾天气持续笼罩我国大部分地区,困扰着广大市民的生活,口罩市场出现热销,小明的爸爸用12000元购进甲、乙两种型号的口罩在自家商店销售,销售完后共获利2700元,进价和售价如表:
(1)小明爸爸的商店购进甲、乙两种型号口罩各多少袋?
(2)该商店第二次以原价购进甲、乙两种型号口罩,购进甲种型号口罩袋数不变,而购进乙种型号口罩袋数是第一次的2倍,甲种口罩按原售价出售,而效果更好的乙种口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋乙种型号的口罩最多打几折?
| 品名 价格 | 甲型口罩 | 乙型口罩 |
| 进价(元/袋) | 20 | 30 |
| 售价(元/袋) | 25 | 36 |
(2)该商店第二次以原价购进甲、乙两种型号口罩,购进甲种型号口罩袋数不变,而购进乙种型号口罩袋数是第一次的2倍,甲种口罩按原售价出售,而效果更好的乙种口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋乙种型号的口罩最多打几折?
11.观察下列图形,照此规律,第5个图形中白色三角形的个数是( )


| A. | 81 | B. | 121 | C. | 161 | D. | 201 |

 如图,过x轴上一点A作平行于y轴的直线分别与抛物线y=$\frac{1}{4}$x2及y=x2交于B、C两点,若正方形BCDE的一边DE与y轴重合,则此正方形BCDE的面积为$\frac{16}{9}$.
如图,过x轴上一点A作平行于y轴的直线分别与抛物线y=$\frac{1}{4}$x2及y=x2交于B、C两点,若正方形BCDE的一边DE与y轴重合,则此正方形BCDE的面积为$\frac{16}{9}$.