题目内容
14. 如图,过x轴上一点A作平行于y轴的直线分别与抛物线y=$\frac{1}{4}$x2及y=x2交于B、C两点,若正方形BCDE的一边DE与y轴重合,则此正方形BCDE的面积为$\frac{16}{9}$.
如图,过x轴上一点A作平行于y轴的直线分别与抛物线y=$\frac{1}{4}$x2及y=x2交于B、C两点,若正方形BCDE的一边DE与y轴重合,则此正方形BCDE的面积为$\frac{16}{9}$.
分析 根据题意可以求得点B和点C的坐标,从而可以得到点B到y轴的距离等于线段BC的长,从而可以求得正方形的边长,进而求得正方形的面积.
解答 解:设点A的坐标为(a,0),
由题意可得,点B的坐标为(a,$\frac{1}{4}$a2),点C的坐标为(a,a2),
∴a=a2-$\frac{1}{4}{a}^{2}$,
解得,a1=0(舍去),a2=$\frac{4}{3}$,
∴正方形BCDE的面积是:$\frac{4}{3}×\frac{4}{3}=\frac{16}{9}$,
故答案为:$\frac{16}{9}$.
点评 本题考查二次函数图象上点的坐标特征、正方形的性质,解题的关键是明确题意,求出正方形的边长.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
4.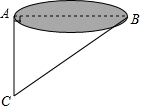 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.| A. | 75•sin55° | B. | 75•cos55° | C. | 75•tan55° | D. | $\frac{75}{tan55°}$ |

 如图,函数y1=2x+m与y2=kx-1的图象相交于点A(-1,a),当-1<kx-1<2x+m时,x的取值范围是-1<x<0.
如图,函数y1=2x+m与y2=kx-1的图象相交于点A(-1,a),当-1<kx-1<2x+m时,x的取值范围是-1<x<0.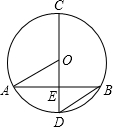 已知:如图,在⊙O中,直径CD交弦AB于点E,且CD平分弦AB,连接OA,BD.
已知:如图,在⊙O中,直径CD交弦AB于点E,且CD平分弦AB,连接OA,BD.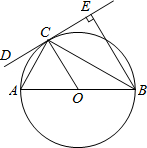 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.